АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

Алгебраическое дополнение		Дискретная случайная величина
Асимптоты графика функции		Дисперсионный анализ
Аффинное преобразование пространства		Евклидово пространство
Базисный минор
Базис в пространстве		Законы распределения случайных величин
Базис на плоскости		Закон больших чисел
Базис на прямой		Знакочередующиеся ряды
Бесконечно малая последовательность		Знакопеременные ряды
Бесконечно малая функция		Испытание
Бесконечно большая функция		Интервальная статистическая оценка
Биномиальное распределение вероятностей		Исследование функции
Вектор		Исследование кривых второго порядка
Векторное пространство		Инварианты поверхности второго порядка
Векторное произведение векторов		Касательная плоскости в точке
Вероятность		Классификация точек разрыва
Вероятность попадания случайной величины в заданный интервал		Криволинейный интеграл
Второй замечательный предел		Компланарные вектора
Выборочная средняя		Комплексное число
Выборочная дисперсия		Комбинаторика
Выборочное корреляционное отношение		Коэффициент вариации
Выборочная совокупность		Корреляционная зависимость
Гармонический ряд		Корреляционный момент
Граф		Коэффициент корреляции
График функции		Коллинеарные вектора
Градиент		Критическая область
Генеральная совокупность		Критерий Пирсона
Гипербола		Критерий Колмогорова
Гистограмма		Критерий Вилкоксона
Двойной интеграл		Линейные операции над векторами
Двухфакторный дисперсионный анализ		Линейная парная регрессия
Декартова система координат		Матрица
Длина вектора		Матричный способ решения систем
Длина дуги кривой		Математическое ожидание дискретной случайной величины
Доверительный интервал для математического ожидания		Математическое ожидание непрерывной случайной величины
Диагональные элементы матрицы		Метод Гаусса
Дисперсия дискретной случайной величины		Медиана
Дисперсия непрерывной случайной величины		Множество
Дифференциал функции		Мода
Дифференциальное уравнение		Момент инерции
Мощность критерия		Плоскость
Минор матрицы		Правила дифференцирования
Необходимый признак сходимости ряда		Правило Лопиталя
Непрерывная функция		Правило трех сигм
Непрерывная случайная величина		Предел последовательности
Неравенство Маркова		Предел функции
Неравенство Чебышева		Работа переменной силы
Несобственный интеграл		Равномерное распределение
Нормальный вектор плоскости		Радиус сходимости степенного ряда
Нормальное уравнение плоскости		Ранг матрицы
Нормальный закон распределения		Ранговая корреляция
Обобщенно гармонический ряд		Расстояние от точки до прямой
Объем совокупности		Расстояние от точки до плоскости
Область определения функции		Расположение поверхностей второго порядка
Область сходимости степенного ряда		Размещения
Область принятия гипотезы		Решение дифференциального уравнения
Обратная функция		Решение системы
Область принятия гипотезы		Ряд Фурье
Объем тел вращения		Ряд Маклорена
Обратная матрица		Ряд Тейлора
Однородные системы уравнений		Сумма ряда
Однородные дифференциальные уравнения		Система дифференциальных уравнений
Однофакторный дисперсионный анализ		Скалярное произведение векторов
Определенный интеграл		Случайная величина
Относительная частота появления события		Случайное событие
Окружность		Смешанное произведение векторов
Парабола		Собственный вектор матрицы
Переменная величина		Совместная система уравнений
Перестановки		Совместные события
Первообразная функции		Сочетания
Первый замечательный предел		Состоятельная статистическая оценка
Периодическая функция		Среднее квадратическое отклонение
Производная функции		Статистическое распределение выборки
Производная сложной функции нескольких переменных		Статистическая гипотеза
Признак сравнения рядов		Статистический критерий
Признак Даламбера		Сходящаяся последовательность
Признак Коши		Теорема Лапласа
Признак Лейбница		Теорема Кронекера-Капелли
Полный дифференциал функции нескольких переменных		Теорема Ферма
Полярные координаты		Теорема Ролля
Подмножество не		Теорема Ляпунова
Постоянная величина		Теорема Коши
Поток событий		Теорема Абеля
Показательный закон распределения		Теорема Эйлера
Правило трех сигм		Теорема умножения вероятностей
Полигон		Теорема сложения вероятностей
Транспонирование матриц		Числовая последовательность
Тригонометрический ряд
Угол между прямыми		Числовой ряд
Угол между плоскостями		Эквивалентные матрицы
Угол между кривыми		Экстремум функции
Умножение матриц		Экстремум функции нескольких переменных
Условная вероятность		Элементы матрицы
Уравнение нормали к плоскости		Элементарные преобразования матрицы
Уравнение касательной		Элементарные дроби
Уравнение нормали		Эллипс
Уравнение прямой на плоскости		Эмпирическая функция распределения
Уравнение прямой в пространстве		Эффективная статистическая оценка
Формулы Крамера
Формула Тейлора
Формула Бернулли
Формула Грина
Формула полной вероятности
Формула Байеса
Формула Стерджеса
Формула Пуассона
Формула интегрирования по частям
Формула Ньютона-Лейбница
Функциональный ряд
Функция распределения вероятностей
Функция плотности распределения вероятностей
Центр тяжести плоской фигуры

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Боровков, А. А. Математическая статистика : учебное пособие. – М. : Лань, 2010. – 704 с.

2. Бунтова, Е. В. Статистическая обработка результатов измерений : учебное пособие. – Самара : РИЦ СГСХА, 2011. – 87 с.

3. Бунтова, Е. В. Теория вероятностей : учебно-методическое пособие. – Самара, 2004. – 169 с.

4. Вентцель, Е. С. Теория случайных процессов и ее инженерные приложения : учебное пособие / Е. С. Вентцель, А. А. Овчаров. – М. : Высшая школа, 2007. – 480 с.

5. Выгодский, М. Я. Справочник по высшей математике. – М. : Наука, 1969. – 872 с.

6. Гмурман, В. Е. Теория вероятностей и математическая статистика : учебное пособие. – М. : Высшая школа, 1977. – 479 с.

7. Гнеденко, Б. В. Курс теории вероятностей : учебник. – М. : Технико-теоретическая литература, 1954. – 411 с.

8. Григорьев, С. Г. Математика : учебное пособие/ С. Г. Григорьев, С. В. Задулина. – М. : Академия, 2005. – 384 с.

9. Данко, П. Е. Высшая математика в упражнениях и задачах : учебное пособие / П. Е. Данко, А. Г. Попов. – М. : Высш. шк., 1999. – Т.1. – 416 с.

10. Данко, П. Е. Высшая математика в упражнениях и задачах : учебное пособие / П. Е. Данко, А. Г. Попов. – М. : Высш.шк., 1999. – Т.2. – 416 с.

11. Канатников, А. Н. Аналитическая геометрия : учебник / А. Н. Канатников, А. П. Крищенко. – М. : МГТУ им Н.Э. Баумана, 2000. – 388 с.

12. Кремер, Н. Ш. Теория вероятностей и математическая статистика : учебное пособие. – М. : ЮНИТИ-ДАНА, 2003. – 543 с.

13. Кудрявцев, В. А. Краткий курс высшей математики : учебное пособие. – М. : Наука, 1975. –624 с.

14. Письменный, Д. Конспект лекций по теории вероятностей и математической статистике. – М. : Айрис-пресс, 2004. –256 с.

15. Пискунов, Н. С. Дифференциальное и интегральное исчисления : учебное пособие. – М. : ФИЗМАТЛИТ, 1996. – 416 с.

16. Романовский, П. И. Общий курс математического анализа в сжатом изложении : учебное пособие. – М. : ФИЗМАТЛИТ, 1962. – 332 с.

17. Рябушко, А. П. Сборник индивидуальных домашних заданий по высшей математике : учебное пособие/ А. П. Рябушко, В. В. Бархатов. – Минск : Высш.шк, 1990. – 352 с.

18. Умнов, А. Е. Аналитическая геометрия и линейная алгебра : лекции. – М. : МФТИ, 2004. – 366 с.

19. Щипачев, В. С. Высшая математика : учебник. – М. : Высш.шк., 2003. – 479 с.

Приложение 1

Таблица значений функции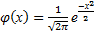


0,0	0,3989
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0	0,2420
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0	0,0540
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9

Приложение 2

Таблица значений функции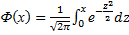

х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
0,00	0,0000	0,26	0,1026	0,52	0,1985	0,78	0,2823
0,01	0,0040	0,27	0,1064	0,53	0,2019	0,79	0,2852
0,02	0,0080	0,28	0,1103	0,54	0,2054	0,80	0,2881
0,03	0,0120	0,29	0,1141	0,55	0,2088	0,81	0,2910
0,04	0,0160	0,30	0,1179	0,56	0,2123	0,82	0,2939
0,05	0,0199	0,31	0,1217	0,57	0,2157	0,83	0,2967
0,06	0,0239	0,32	0,1255	0,58	0,2190	0,84	0,2995
0,07	0,0279	0,33	0,1293	0,59	0,2224	0,85	0,3023
0,08	0,0319	0,34	0,1331	0,60	0,2257	0,86	0,3051
0,09	0,0359	0,35	0,1368	0,61	0,2291	0,87	0,3078
0,10	0,0398	0,36	0,1406	0,62	0,2324	0,88	0,3106
0,11	0,0438	0,37	0,1443	0,63	0,2357	0,89	0,3133
0,12	0,0478	0,38	0,1480	0,64	0,2389	0,90	0,3159
0,13	0,0517	0,39	0,1517	0,65	0,2422	0,91	0,3186
0,14	0,0557	0,40	0,1554	0,66	0,2454	0,92	0,3212
0,15	0,0596	0,41	0,1591	0,67	0,2486	0,93	0,3238
0,16	0,0636	0,42	0,1628	0,68	0,2517	0,94	0,3264
0,17	0,0675	0,43	0,1664	0,69	0,2549	0,95	0,3289
0,18	0,0714	0,44	0,1700	0,70	0,2580	0,96	0,3315
0,19	0,0753	0,45	0,1736	0,71	0,2611	0,97	0,3340
0,20	0,0793	0,46	0,1772	0,72	0,2642	0,98	0,3365
0,21	0,0832	0,47	0,1808	0,73	0,2673	0,99	0,3389
0,22	0,0871	0,48	0,1844	0,74	0,2703	1,00	0,3413
0,23	0,0910	0,49	0,1879	0,75	0,2734	1,01	0,3438
0,24	0,0948	0,50	0,1915	0,76	0,2764	1,02	0,3461
0,25	0,0987	0,51	0,1950	0,77	0,2794	1,03	0,3485
1,04	0,3508	1,34	0,4099	1,64	0,4495	1,94	0,4738
1,05	0,3531	1,35	0,4115	1,65	0,4505	1,95	0,4744
1,06	0,3554	1,36	0,4131	1,66	0,4515	1,96	0,4750
1,07	0,3577	1,37	0,4147	1,67	0,4525	1,97	0,4756
1,08	0,3599	1,38	0,4162	1,68	0,4535	1,98	0,4761
1,09	0,3621	1,39	0,4177	1,69	0,4545	1,99	0,4767
1,10	0,3643	1,40	0,4192	1,70	0,4554	2,00	0,4772
1,11	0,3665	1,41	0,4207	1,71	0,4564	2,02	0,4783
1,12	0,3686	1,42	0,4222	1,72	0,4573	2,04	0,4793
1,13	0,3708	1,43	0,4236	1,73	0,4582	2,06	0,4803
1,14	0,3729	1,44	0,4251	1,74	0,4591	2,08	0,4812
х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
1,15	0,3749	1,45	0,4265	1,75	0,4599	2,10	0,4821


1,16	0,3770	1,46	0,4279	1,76	0,4608	2,12	0,4830
1,17	0,3790	1,47	0,4292	1,77	0,4616	2,14	0,4838
1,18	0,3810	1,48	0,4306	1,78	0,4625	2,16	0,4846
1,19	0,3830	1,49	0,4319	1,79	0,4633	2,18	0,4854
1,20	0,3849	1,50	0,4332	1,80	0,4641	2,20	0,4861
1,21	0,3869	1,51	0,4345	1,81	0,4649	2,22	0,4868
1,22	0,3883	1,52	0,4357	1,82	0,4656	2,24	0,4875
1,23	0,3907	1,53	0,4370	1,83	0,4664	2,26	0,4881
1,24	0,3925	1,54	0,4382	1,84	0,4671	2,28	0,4887
1,25	0,3944	1,55	0,4394	1,85	0,4678	2,30	0,4893
1,26	0,3962	1,56	0,4406	1,86	0,4686	2,32	0,4898
1,27	0,3980	1,57	0,4418	1,87	0,4693	2,34	0,4904
1,28	0,3997	1,58	0,4429	1,88	0,4699	2,36	0,4909
1,29	0,4015	1,59	0,4441	1,89	0,4706	2,38	0,4913
1,30	0,4032	1,60	0,4452	1,90	0,4713	2,40	0,4918
1,31	0,4049	1,61	0,4463	1,91	0,4719	2,42	0,4922
1,32	0,4066	1,62	0,4474	1,92	0,4726	2,44	0,4927
1,33	0,4082	1,63	0,4484	1,93	0,4732	2,46	0,4931
2,48	0,4934	2,66	0,4961	2,84	0,4977	3,20	0,49931
2,50	0,4938	2,68	0,4963	2,86	0,4979	3,40	0,49966

2,52	0,4941	2,70	0,4965	2,88	0,4980	3,60	0,49984
2,54	0,4945	2,72	0,4967	2,90	0,4981	3,80	0,49992
2,56	0,4948	2,74	0,4969	2,92	0,4982	4,00	0,49996
2,58	0,4951	2,76	0,4971	2,94	0,4984	4,50	0,49999
2,60	0,4953	2,78	0,4973	2,96	0,4985	5,00	0,49999
2,62	0,4956	2,80	0,4974	2,98	0,4986
2,64	0,4959	2,82	0,4976	3,00	0,49865

Приложение 3

Таблица значений

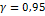
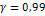
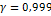
n				n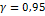
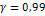
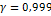
	2,78	4,60	8,61		2,093	2,861	3,883
	2,57	4,03	6,86		2,064	2,797	3,745
	2,45	3,71	5,96		2,045	2,756	3,659
	2,37	3,50	5,41		2,032	2,720	3,600
	2,31	3,36	5,04		2,023	2,708	3,558
	2,26	3,25	4,78		2,016	2,692	3,527
	2,23	3,17	4,59		2,009	2,679	3,502
	2,20	3,11	4,44		2,001	2,662	3,464
	2,18	3,06	4,32		1,996	2,649	3,439
	2,16	3,01	4,22		1,001	2,640	3,418
	2,15	2,98	4,14		1,987	2,633	3,403
	2,13	2,95	4,07		1,984	2,627	3,392
	2,12	2,92	4,02		1,980	2,617	3,374
	2,11	2,90	3,97		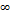1,960	2,576	3,291
	2,10	2,88	3,92

Приложение 4

Таблица значений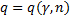

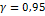
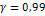
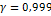
n				n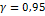
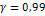
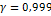
	1,37	2,67	5,64		0,37	0,58	0,88
	1,09	2,01	3,88		0,32	0,49	0,73
	0,92	1,62	2,98		0,28	0,43	0,63
	0,80	1,38	2,42		0,26	0,38	0,56
	0,71	1,20	2,06		0,24	0,35	0,50
	0,65	1,08	1,80		0,22	0,32	0,46
	0,59	0,98	1,60		0,21	0,30	0,43
	0,55	0,90	1,45		0,188	0,269	0,38
	0,52	0,83	1,33		0,174	0,245	0,34
	0,48	0,78	1,23		0,161	0,226	0,31
	0,46	0,73	1,15		0,151	0,211	0,29
	0,44	0,70	1,07		0,143	0,198	0,27
	0,42	0,66	1,01		0,115	0,160	0,211
	0,40	0,63	0,96		0,099	0,136	0,185
	0,39	0,60	0,92		0,089	0,120	0,162

Приложение 5

Критические точки распределения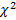

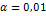
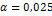
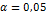
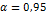
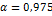
Число степеней свободы k	Уровень значимости	Уровень значимости	Уровень значимости	Уровень значимости	Уровень значимости	Уровень значимости
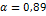
	6,6	5,0	3,8	0,0039	0,00098	0,00016
	9,2	7,4	6,0	0,103	0,051	0,020
	11,3	9,4	7,8	0,352	0,216	0,115
	13,3	11,1	9,5	0,711	0,484	0,297
	15,1	12,8	11,1	1,15	0,831	0,554
	16,8	14,4	12,6	1,64	1,24	0,872
	18,5	16,0	14,1	2,17	1,69	1,24
	20,1	17,5	15,5	2,73	2,18	1,65
	21,7	19,0	16,9	3,33	2,70	2,09
	23,2	20,5	18,3	3,94	3,25	2,56
	24,7	21,9	19,7	4,57	3,82	3,05
	26,2	23,3	21,0	5,23	4,40	3,57
	27,7	24,7	22,4	5,89	5,01	4,11
	29,1	26,1	23,7	6,57	5,63	4,66
	30,6	27,5	25,0	7,26	6,26	5,23
	32,0	28,8	26,3	7,96	6,91	5,81
	33,4	30,2	27,6	8,67	7,56	6,41
	34,8	31,5	28,9	9,39	8,23	7,01
	36,2	32,9	30,1	10,1	8,91	7,63
	37,6	34,2	31,4	10,9	9,59	8,26
	38,9	35,5	32,7	11,6	10,3	8,90
	40,3	36,8	33,9	12,3	11,0	9,54
	41,6	38,1	35,2	13,1	11,7	10,2
	43,0	39,4	36,4	13,8	12,4	10,9
	44,3	40,6	37,7	14,6	13,1	11,5
	45,6	41,9	38,9	15,4	13,8	12,2
	47,0	43,2	40,1	16,2	14,6	12,9
	48,3	44,5	41,3	16,9	15,3	13,6
	49,6	45,7	42,6	17,7	16,0	14,3
	50,9	47,0	43,8	18,5	16,8	15,0

Приложение 6

<238 239 240 241242243 244 >

Дата добавления: 2015-08-11; просмотров: 1156;