Занятие №55. Корреляционный анализ

Продолжение выполнения типового задания.

Проведем корреляционный анализ случайных величин X и Y. Выясним, существует ли корреляционная зависимость между случайными величинами X и Y, при которой изменение одной из величин влечет изменение среднего значения другой.

Пусть случайная величина Y – урожай зерна, а случайная величина X – количество внесенных удобрений. Функция Y не является функцией от X, так как с одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай. Но средний урожай является функцией от количества удобрений, т.е. Y связан с X корреляционной зависимостью.

Для описания системы двух случайных величин используют такие характеристики, как корреляционный момент 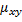и коэффициент корреляции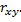

Корреляционным моментом 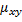случайных величин X и Y называют математическое ожидание произведения отклонений этих величин. Для вычисления корреляционного момента используют формулу

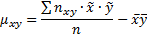
Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент равен нулю, если X и Y независимы, X и Y зависимые случайные величины, если корреляционный момент не равен нулю.

Коэффициентом корреляции независимых случайных величин X и Y называют отношение корреляционного момента к произведению среднеквадратических отклонений этих величин

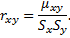
Коэффициент корреляции независимых случайных величин равен нулю.

Найдем корреляционный момент, для чего составим вспомогательную таблицу

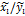
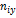
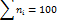
Вычислим

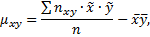
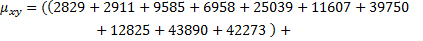
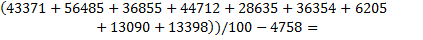
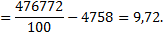
Вычислим

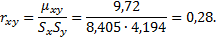
Можно сделать вывод, что случайные величины X и Y зависимые. Одну из величин представим как функцию другой. Так как точное приближение невозможно, то ограничимся приближенным представлением величины Y в виде линейной функции величины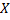

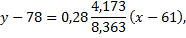
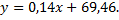
Данное уравнение прямой называют уравнением среднеквадратической регрессии 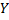на .

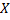Аналогично записывают уравнение прямой – среднеквадратической регрессии 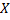на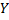

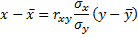
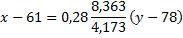
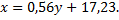
Обе прямые регрессии проходят через точку 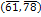, которую называют центром совместного распределения величин 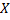и .

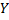Проверим гипотезу о значимости выборочного коэффициента корреляции. Выборка отобрана случайно, следовательно, нельзя утверждать, что коэффициент корреляции генеральной совокупности отличен от нуля. Это является причиной того, что необходимо при заданном уровне значимости 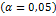проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции 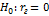при конкурирующей гипотезе .

В качестве критерия проверки нулевой гипотезы принимают случайную величину

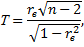
которая при справедливости нулевой гипотезы имеет распределение Стьюдента с 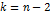степенями свободы.

Вычислим наблюдаемое значение критерия

По таблице критических точек распределения Стьюдента (прил. 9), по заданному уровню значимости 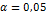и числу степеней свободы 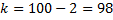найдем критическую точку .

Так как 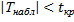, то нет оснований отвергнуть нулевую гипотезу.

Построим корреляционное поле, на котором изобразим линии регрессии

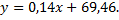
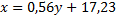
и «облако» корреляции.

Чтобы построить линию регрессии 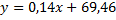составим вспомогательную таблицу

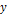
	75,2	80,38

Чтобы построить линию регрессии 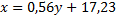составим вспомогательную таблицу

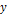
	55,87	65,95

Построим графики линий регрессии (рис. 83).

Рис. 83