Занятие №54. Эмпирические и выравнивающие частоты. Статистическая проверка гипотез

Продолжение выполнения типового задания.

5) Найдем выравнивающие (теоретические) частоты. Для этого составим вспомогательную таблицу

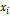
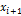
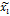
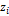
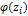
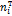
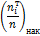
			-2,39	0,0229	1,095	0,01	0,01
			-1,91	0,0644	3,080	0,03	0,04
			-1,44	0,1445	6,768	0,07	0,11
			-0,96	0,2516	12,03	0,12	0,23
			-0,48	0,3555	17,00	0,17	0,40
				0,3989	19,08	0,19	0,59
			0,48	0,3555	17,00	0,17	0,76
			0,96	0,2516	12,03	0,12	0,88
			1,44	0,1415	6,768	0,07	0,95
			1,91	0,0644	3,080	0,03	0,98

где

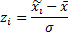
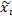– середина интервала, 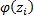– функция Лапласа (прил. 2), 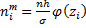– теоретические частоты.

По выстроенному интервальному статистическому ряду и выравнивающим относительным частотам построим график, который будет определять вид функции плотности распределения выравнивающих относительных частот (рис. 74 (y2)).

По выстроенному интервальному статистическому ряду и накопленным выравнивающим относительным частотам построим график, который будет определять вид функции распределения выравнивающих относительных частот (рис. 75 (y2)).

Построенные графики относительных частот дают возможность выдвинуть гипотезу о законе распределения случайной величины 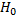: случайная величина Х распределена по нормальному закону с 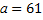и .

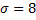6)С помощью критерия Пирсона проверим правильность выдвинутой гипотезы .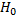

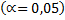Согласно критерию, необходимо найти

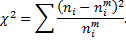
Построим вспомогательную таблицу.

Интервалы, содержащие малочисленные эмпирические частоты следует объединить, а частоты этих интервалов сложить.

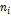
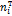
	1,09	3,08	6,768	12,03	17,00	19,079	17,00	12,03	6,77	3,08

После объединения интервалов получим следующий ряд

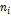
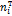
	4,18	6,77	12,03	17,00	19,08	17,00	12,03	9,85

Рассчитаем :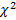

.

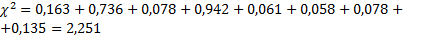По таблице критических точек 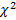(прил. 6), по заданному уровню значимости и числу степеней свободы 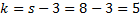, s – число интервалов после объединения, находим критическую точку

.

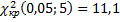Так как , то нет снований отвергнуть гипотезу о нормальном распределении генеральной совокупности.

7)Одного критерия недостаточно для проверки нулевой гипотезы 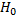. Проверим выдвинутую гипотезу с помощью критерия Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распределения и соответствующей теоретической функцией распределения, которой называют статистику критерия Колмогорова

.

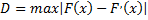Построим вспомогательную таблицу

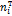
	1,09	3,08	6,77	12,03	17,00	19,08	17,00	12,03	6,77	3,08
	0,45	0,03	0,25	0,07	0,31	0,06	0,06	0,07	0,03	0,23

По эмпирическим данным рассчитывается распределение

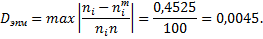
По заданному объему выборки 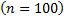и уровню значимости 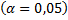определяем табличное значение 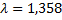(при 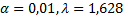) и находим .

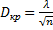В нашем случае 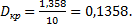Так как 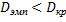, то нулевую гипотезу принимают.

Аналогично проводят статистическую обработку данных случайной величины Y.