Занятие №53. Статистические оценки параметров распределения

Продолжение выполнения типового задания.

3) Найдем интервальные оценки параметров распределения.

Интервал для математического ожидания

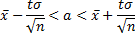
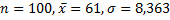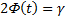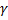В нашем случае , t находим из равенства , где – заданная надежность 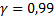, 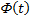– функция Лапласа (прил. 3) .

.

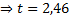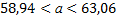Интервал для СКО

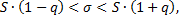
где 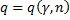– табличное значение (прил.5) .

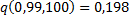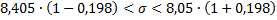
4) Построим интервальный статистический ряд распределения по эмпирическим данным выборки.

Желательно, чтобы длина интервала 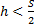. В наше случае 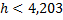, возьмем .

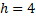Определим :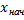

.

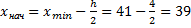Последний интервал включает в себя .

Построим интервальный ряд распределения:

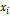
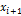
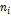
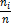
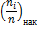
			0,02	0,02
			0,03	0,05
			0,09	0,14
			0,13	0,27
			0,13	0,4
			0,18	0,58
			0,18	0,76
			0,13	0,89
			0,07	0,96
			0,04

5)По выстроенному интервальному статистическому ряду и эмпирическим относительным частотам построим график, который будет определять вид функции плотности распределения относительных частот (рис. 81 (y1)).

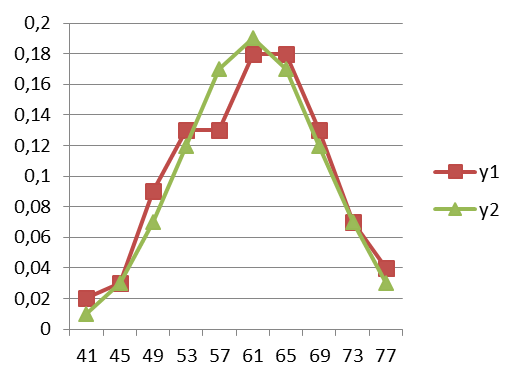
Рис. 81

По выстроенному интервальному статистическому ряду и накопленным эмпирическим относительным частотам построим график, который будет определять вид функции распределения относительных частот (рис. 82 (y1)).

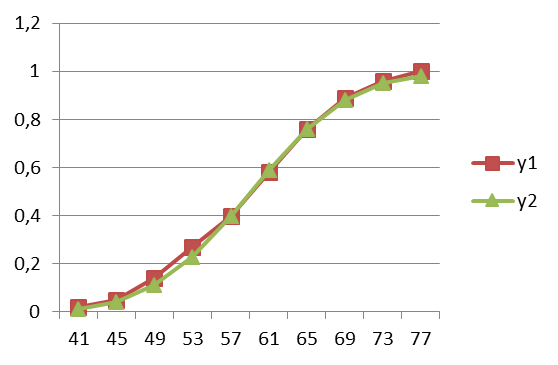
Рис. 82