Занятие №51. Законы распределения непрерывной случайной величины

Равномерный закон распределения.

№6. На шоссе установлен автоматический светофор, в котором 1 минуту для транспорта горит зеленый цвет и 45 секунд – красный, затем опять 1 минуту горит зеленый и 45 секунд – красный и т.д. Автомашина проезжает по шоссе в случайный момент времени, не связанный с работой светофора. Найти вероятность того, что машина проедет мимо светофора не останавливаясь.

Примечание: случайная величина 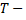момент времени проезда автомашины мимо светофора в интервале, равном периоду смены цветов в светофоре.

Период смены цветов распределена равномерно на отрезке

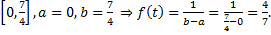
Вне этого отрезка

Нормальный закон распределения.

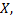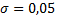№7. На станке изготавливают шарик для подшипников. Номинальный диаметр шарика мм. Фактический размер диаметр шарика вследствие неточности изготовления представляет собой случайная величина распределенная по нормальному закону с математическим ожиданием мм и средним квадратическим отклонением мм.

Найти: Процент шариков для подшипников, которые будут иметь диаметр от 4,8 до 5 мм. Процент брака, если известно, что при контроле бракуются все шарики, диаметр которых отклоняется от номинального по абсолютной величине больше, чем на 0,1 мм.

Примечание:

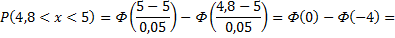
так как

Вывод: 50% изготовленных шариков для подшипников будут иметь диаметр от 4,8 до 5 мм.

Пусть шарик забракован, шарик не будет забракован

, тогда

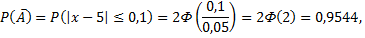
так как

Вывод: бракуют 4,56% изготовленных шариков.

№8. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону распределения со средним квадратическим отклонением 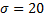грамм. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 грамм.

Примечание: случайная величина 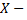случайные ошибки взвешивания. Математическое ожидание

Показательный закон распределения.

№9. Случайная величина распределена по показательному закону, заданному плотностью распределения вероятностей при 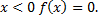Найти вероятность т ого, что в результате испытания примет значение из интервала

Примечание:

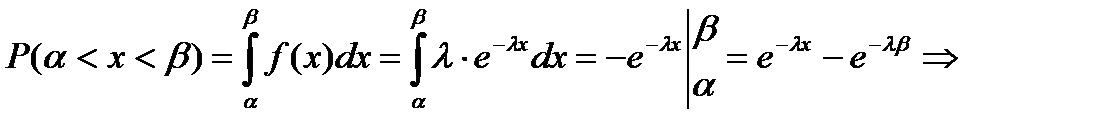
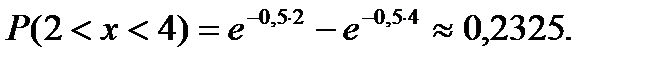
№10. Продолжительность безотказной работы элемента – случайная величина, распределенная по показательному закону, заданная плотность распределения вероятностей 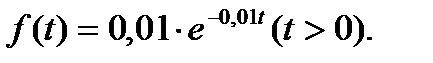Найти вероятность того, что элемент проработает безотказно не менее 100 часов.

Примечание: пусть 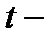непрерывная случайная величина (продолжительность безотказной работы элемента). Продолжительность безотказной работы элемента не менее 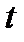часов определяется с помощью функции надежности

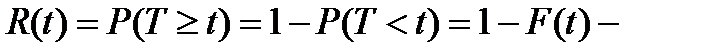
это есть функция распределения, для показательного закона

т.е. 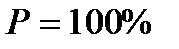что элемент проработает не менее 100 часов.

№11. Испытывают два независимо работающих элемента. Продолжительность безотказной работы первого и второго элементов – случайная величина распределенные по показательному закону, эти величины характеризуются функциями распределения

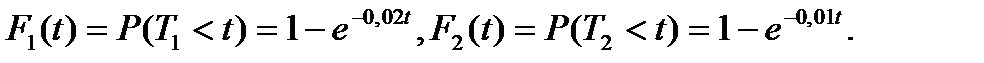
Найти вероятность того, что в интервале времени (0;100) часов:

а) оба элемента откажут;

б) только один элемент откажет.