Аналитическая реализация непрерывной линейной математической модели

Решение ЛНДУ 2-го порядка с постоянными коэффициентами

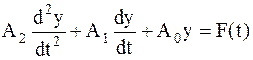(32)

в общем случае представляется в виде , где 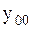— общее решение соответствующего ЛОДУ, 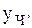— какое-либо частное решение ЛНДУ. В силу простоты функции

F(t) = B = Const для 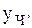имеем:

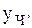= Const .

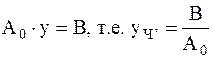Таким образом, общее решение ЛНДУ:

.

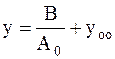Решение соответствующего ЛОДУ могут быть определены как:

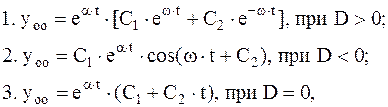
в зависимости от решений характеристического уравнения вида:

,

где 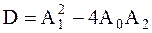— дискриминант характеристического уравнения. Отсюда,

.

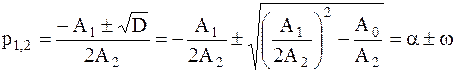Таким образом, параметры решения есть

Однако и знак дискриминанта определяет лишь вид решения.

Неизвестные коэффициенты С₁ и С₂ определяются из условий задачи Коши:

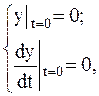
и имеют вид:

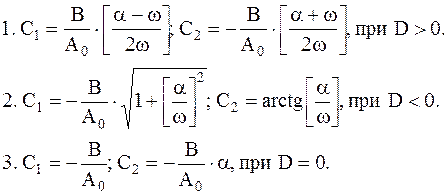
Переходя от абстрактной математической модели к рассмотрению механической и электрической систем, можно определить соответствия параметров решения:

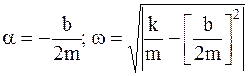— для пружинного маятника;

— для электрического контура.