Анализ поведения динамического элемента. В зависимости от значений параметров модели определяется форма решения:

В зависимости от значений параметров модели определяется форма решения:

I. При D > 0:

1. , 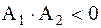— апериодическое расходящееся;

2. , 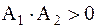— апериодическое сходящееся.

II. При D < 0:

1. 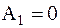— гармоническое;

2. 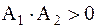— периодическое сходящееся;

3. 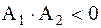— периодическое расходящееся.

III. При D = 0:

1. 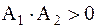— сходящееся;

2. 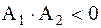— расходящееся.

Соответствующие семейства кривых, отражающие влияние параметров на форму решения, представлены в графическом приложении 1.

Практически в реальных физических системах возможна реализация условий функционирования, соответствующих неотрицательным значениям параметров математической модели. Таким образом, на математическую модель накладываются естественные ограничения:

1. функция может являться периодической сходящейся;

2. функция может являться апериодической сходящейся.