Аналитическая реализация непрерывной нелинейной математической модели
Уравнение Ван дер Поля не имеет общего решения, которое можно было бы представить аналитически; существуют различные приближенные методы для оценки его вида (например, приближенный метод Ляпунова — Боголюбова). Однако наиболее удобным и обобщенным является использование фазовой плоскости для анализа поведения решения в окрестности некоторой точки.
Принципиально выделяется 2 вида точек фазовой плоскости:
1. обыкновенные точки;
2. особые точки (точки покоя).
Обыкновенные точки характеризуются единственностью проходящих через них фазовых траекторий, в то время как особые точки позволяют выделить семейства фазовых траекторий и поэтому представляют больший интерес.
В общем случае нелинейное дифференциальное уравнение второго порядка имеет вид:
 (37)
(37)
равносильно системе уравнений второго порядка
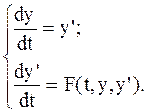 (38)
(38)
Общее решение системы y = y(t), y’ = y’(t) может быть представлено геометрически семейством ориентированных фазовых траекторий на фазовой плоскости Oyy’.
Применительно к уравнению Ван дер Поля получается автономная система дифференциальных уравнений, т.е. система, в которой функции Q(y, y’) и P(y, y’) явно не зависят от параметра t:
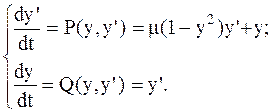 (39)
(39)
Для возможности исследования автономной системы ее следует линеаризовать в точке покоя.
При этом, если у автономной системы существует точка покоя, то
P(y, y’) = Q(y, y’) = 0. (40)
Очевидно, что для уравнения Ван дер Поля это условие выполняется в точке (0,0).
Линеаризация заключается в разложении правых частей дифференциальных уравнений системы по формуле Тейлора. Тогда для эквивалентной уравнению Ван дер Поля системы получим:
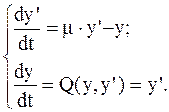 (41)
(41)
Характер точки покоя полученной системы зависит от корней характеристического уравнения:
 (42)
(42)
т.е., определяется значением коэффициента .
Характер фазовой траектории в окрестности обыкновенной точки определяется только характером полученных траекторий в точке покоя, т.е. при фиксированном невозможно выделить точки на плоскости, в окрестностях которых фазовая траектория будет иметь характер, отличный от траектории в точке покоя.
Замечание: при анализе характера точки покоя в случае 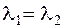 , следует учитывать, что матрица А характеристического уравнения является недиагонализуемой, т.е. не существует матрицы С такой, что
, следует учитывать, что матрица А характеристического уравнения является недиагонализуемой, т.е. не существует матрицы С такой, что
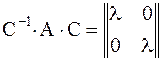 или
или 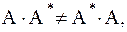 (43)
(43)
где 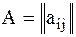 и
и 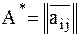 эмиртовые матрицы (точнее матрица А диагонализуема только в случае = 0).
эмиртовые матрицы (точнее матрица А диагонализуема только в случае = 0).
Дата добавления: 2015-07-30; просмотров: 1044;
