Интерпретация концептуальной модели в математическое описание динамического элемента с запаздыванием
Математическое описание линейного динамического элемента с запаздыванием задается в общем случае линейным дифференциальным уравнением n-го порядка :
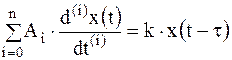 , (44)
, (44)
| где: | k | — | коэффициент затухания, |
| — | параметр, характеризующий время запаздывания, | ||
| n | — | число слагаемых уравнения, задаваемое дополнительными условиями. |
Объект представляет собой систему, подвергающуюся воздействию внешних факторов и вырабатывающую на них соответствующие отклики, причем запаздывание может быть учтено разбиением его на две части (рис. 5).
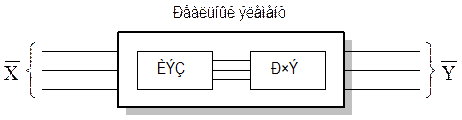
Рис. 5. Моделируемый объект с запаздыванием
При этом: ИЭЗ — идеальный элемент запаздывания, РЧЭ — реальная часть элемента,
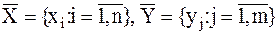 . (45)
. (45)
Уравнение функционирования идеальной части имеет вид:
y(t) = x(t–). (46)
Реальная часть элемента характеризуется коэффициентом затухания k, который представляет собой постоянное возмущение, действующее на динамический элемент.
Вообще говоря, любой элемент определенной структуры осуществляет преобразование входного сигнала в выходной, т.е. является оператором преобразования и имеет передаточную функцию. Передаточная функция представляет некоторый линейный оператор, который преобразует внешнюю нагрузку на входе в нормальную реакцию на выходе.
Передаточная функция представляется отношением:
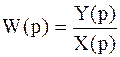 , (47)
, (47)
где Y(p) и X(p) — соответственно изображения функций y(t) и x(t) ( преобразование Лапласа ).
Для идеального запаздывания передаточная функция равна:
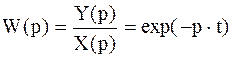 . (48)
. (48)
Таким образом, запаздывание в динамическом элементе моделируется в пространстве изображений, а не оригиналов.
Дифференциальное уравнение первого (28) и второго (29) порядков, описывающие поведение динамического элемента без запаздывания, с учетом запаздывания примут вид уравнений (30) и (31) соответственно.
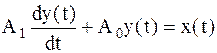 , (49)
, (49)
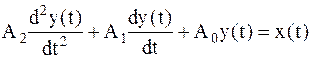 , (50)
, (50)
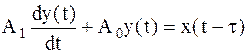 , (51)
, (51)
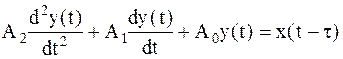 . (52)
. (52)
В уравнениях (30) и (31) t .
Дата добавления: 2015-07-30; просмотров: 895;
