Анализ поведения динамического элемента

В зависимости от значений параметров модели определяется форма решения на фазовой плоскости:

I. Действительные корни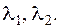

1. :

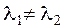1.1. 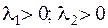— неустойчивый узел;

1.2. 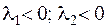— ассимптотически устойчивый узел;

1.3. — неустойчивое седло.

2. :

2.1. 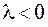— ассимптотически устойчивый вырожденный узел;

2.2. 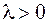— ассимптотически неустойчивый вырожденный узел.

II. Комплексные корни .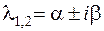

1. 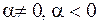— ассимптотически устойчивый фокус;

2. 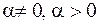— неустойчивый фокус;

3. 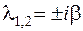— устойчивый центр.

Соответствующие семейства кривых, отражающие влияние параметров на форму решения, представлены в графическом приложении 2.

Практически в реальных физических системах возможна реализация условий функционирования, соответствующих неотрицательным значениям параметра m. Таким образом, на математическую модель накладываются естественные ограничения в фазовой плоскости:

1. точка покоя является неустойчивым фокусом;

2. точка покоя является ассимптотически неустойчивым вырожденным узлом;

3. точка покоя является неустойчивым узлом.