Анализ поведения динамического элемента. Используем в качестве математической модели запаздывания разложение в ряд Падэ.
Используем в качестве математической модели запаздывания разложение в ряд Падэ.
В случае n = m = 0 имеем вырожденный случай, когда никакого запаздывания нет, т.е. W (p) = 1. В случае n = m = 1 имеем
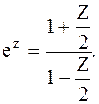
Т.к. Z = p , то
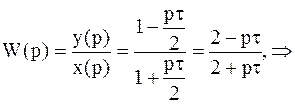

Переходя к оригиналам и полагая y(0) = 0 и x(0) = 0, имеем
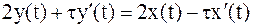 .
.
Поскольку x(t) = Сonst = k, то  и, следовательно, данное уравнение преобразуется к следующему виду:
и, следовательно, данное уравнение преобразуется к следующему виду:
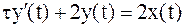 или
или 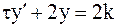 .
.
Уравнение 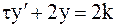 является линейным неоднородным дифференциальным уравнением первого порядка с постоянными коэффициентами. Его решение ищем в виде
является линейным неоднородным дифференциальным уравнением первого порядка с постоянными коэффициентами. Его решение ищем в виде 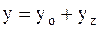 , где
, где 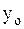 — решение соответствующего однородного дифференциального уравнения, а
— решение соответствующего однородного дифференциального уравнения, а 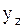 — частное решение данного уравнения.
— частное решение данного уравнения.
Характеристическое уравнение имеет вид:
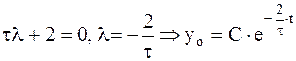 .
.
Нетрудно видеть, что решение y = k является частным решением данного уравнения. Таким образом,
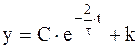 .
.
Для определения значения постоянной С воспользуемся тем обстоятельством, что y(0) = 0. Следовательно, y(0) = C + k = 0 и C = – k. Таким образом, окончательно имеем
 .
.
Это уравнение представляет собой уравнение апериодического сходящегося процесса.
В случае n = m = 2 порядок изложения аналитической реализации модели аналогичен. Таким образом, имеем
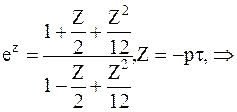
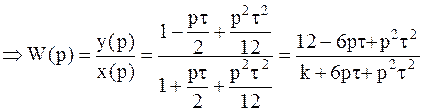 ,
,
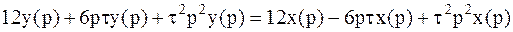 .
.
Полагаем, что 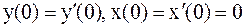 . Переходя к оригиналам, имеем:
. Переходя к оригиналам, имеем:
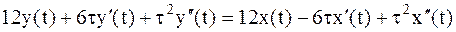 .
.
Т.к. x(t) = Сonst = k, то
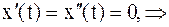
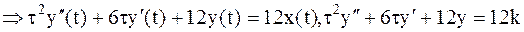 .
.
Характеристическое уравнение имеет вид :
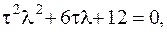

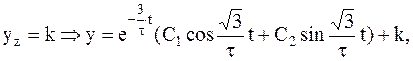
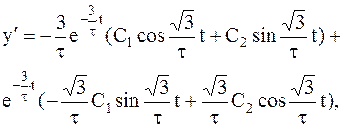
т.к. 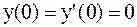 , то имеем систему:
, то имеем систему:
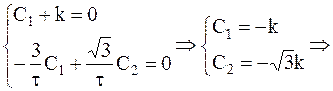
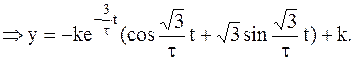
Полученное уравнение представляет собой уравнение периодического сходящегося процесса.
Соответствующие семейства кривых, отражающие влияние параметров на форму решения, представлены в графическом приложении 3.
Практически в реальных физических системах возможна реализация условий функционирования, соответствующих неотрицательным значениям параметров математической модели. Таким образом, на математическую модель накладываются естественные ограничения:
1. функция может являться периодической сходящейся;
2. функция может являться апериодической сходящейся.
Дата добавления: 2015-07-30; просмотров: 1218;
