Электрическая модель

Примером электрической цепи, в которой могут происходить свободные электрические колебания, служит простейший колебательный контур (рис. 3), состоящий из конденсатора С и соединенной с ним последовательно катушки индуктивности L. Если линейные размеры контура l не слишком велики (l << c/, где с= 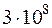м/c — скорость света в вакууме, — частота колебаний в контуре), то можно считать, что в каждый момент времени t сила тока I во всех частях контура одинакова.

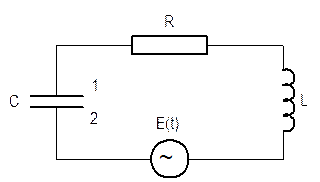
Рис. 3. Электрический колебательный контур

Для осуществления вынужденных колебаний в электрическом колебательном контуре в него нужно включить источник электрической энергии, ЭДС Е(t) которого изменяется с течением времени.

По закону Ома для участка цепи 1–R–L–2 квазистационарного тока, возникающего в контуре при вынужденных колебаниях,

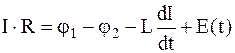. (30)

Здесь — разность потенциалов обкладок конденсатора, q — его заряд, а внутреннее электрическое сопротивление источника ЭДС считается пренебрежимо малым по сравнению с R.

Из закона сохранения электрического заряда следует, что 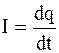. Поэтому дифференциальное уравнение вынужденных электрических колебаний в контуре можно представить в форме:

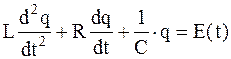. (31)