Интерпретация концептуальной модели в математическое описание динамического элемента
Математическое описание системного элемента, задаваемое линейным дифференциальным уравнением второго порядка с правой частью, имеет вид:
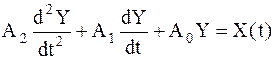 , (28)
, (28)
где X, Y и t выполняют роль параметров 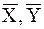 и T из формулы (1),
и T из формулы (1), 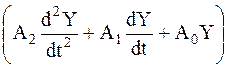 — функция преобразования F,
— функция преобразования F, 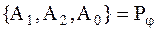 — функциональные параметры.
— функциональные параметры.
Функциональные параметры могут быть:
1. постоянными — 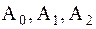 = Const;
= Const;
2. переменными — 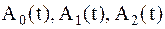 . Следует отметить, что коэффициент
. Следует отметить, что коэффициент 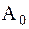 характеризует упругие свойства объекта,
характеризует упругие свойства объекта, 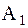 отображает фрикционные силы объекта (силы трения), а коэффициент
отображает фрикционные силы объекта (силы трения), а коэффициент 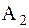 отображает инерционные свойства объекта моделирования.
отображает инерционные свойства объекта моделирования.
Объект представляет собой систему, подвергающуюся воздействию внешних факторов и вырабатывающую на них соответствующие отклики (рис. 2).

Рис. 2. Объект моделирования
При этом 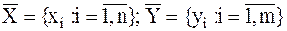 .
.
Дата добавления: 2015-07-30; просмотров: 737;
