Занятие №48. Повторные независимые испытания
№1. В семье трое детей. Какова вероятность того, что: а) все они мальчики; б) один мальчик и две девочки. Считать вероятность рождения мальчика 0,51, а девочки – 0,49.
Примечание: a) в данном случае используем формулу Бернулли, учитывая, что 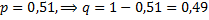 , получим
, получим
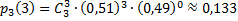 .
.
б) Искомая вероятность находится по теореме умножения, так как интересует одновременное появление событий:  в семье имеется 1 мальчик и
в семье имеется 1 мальчик и 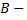 в семье имеется 2 девочки. Вероятность события
в семье имеется 2 девочки. Вероятность события  и вероятность события
и вероятность события 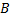 найдем по формуле Бернулли:
найдем по формуле Бернулли:
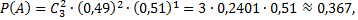
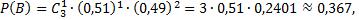
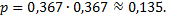
№2. Прибор состоит из 10 узлов. Надежность (вероятность безотказной работы в течении времени 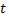 ) для каждого узла равна
) для каждого узла равна 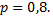 Узлы выходят из строя независимо один от другого. Найти вероятность того, что за время
Узлы выходят из строя независимо один от другого. Найти вероятность того, что за время 
а) откажет хотя бы один узел;
б) откажет ровно один узел;
в) откажут ровно два узла;
г) откажут не менее двух узлов;
д) откажут от 4 до 6 узлов.
Примечание: a) 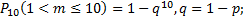
б) 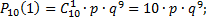
в) 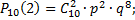
г) 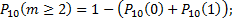
д) 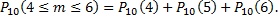
№3. Вероятность наступления события  в каждом из 100 независимых испытаний равна 0,8. Найти вероятность того, что событие
в каждом из 100 независимых испытаний равна 0,8. Найти вероятность того, что событие  наступит:
наступит:
а) ровно 84 раза;
б) не менее 72 и не более 84 раза.
Примечание: задача состоит в том, что необходимо найти вероятность появления определенного количества интересующих исходов (84) из всех возможных исходов (100). Так как общее число испытаний достаточно велико, то стоит применить формулу Лапласа для нахождения вероятности
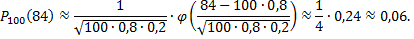
Аналогичные рассуждения указывают на решение второй части вопроса, применяя интегральную формулу Лапласа:

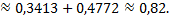
№4. Задачник по теории вероятностей издан тиражом 20 000 экземпляров. Вероятность того, что он сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит три бракованных книги.
Применение: в данном случае вероятность появления интересующего исхода очень мала, а количество проведенных испытаний достаточно велико. Следует проверить, возможно ли использовать формулу Пуассона: 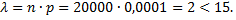 Условие, при котором возможно применение формулы Пуассона выполнено
Условие, при котором возможно применение формулы Пуассона выполнено
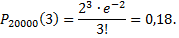
№5. Найти вероятность того, что в партии из 900 изделий число изделий высшего сорта заключено между 600 и 700. Вероятность появления изделия высшего сорта в партии равна 0,8.
№6. Завод отправил на базу 10 000 стаканов. Стаканы разбиваются в пути с вероятностью 0,0002. Какова вероятность того, что в пути разобьется менее трех стаканов?
№7. Среди 5000 семян 0,03% сорняков. Найти вероятность того, что будет найдено не менее двух семян сорняков.
№8. Прибор состоит из 200 деталей, каждая из которых может выйти из строя с вероятностью 0,01. Найти вероятность того, что выйдут из строя не более трех деталей.
№9. На опытной станции посеяно 150 семян кукурузы. Всхожесть семян 95%. Найти вероятность того, что из 150 семян взойдет не менее 90%.
№10. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудет 3 поврежденных изделия.
Дата добавления: 2015-08-11; просмотров: 8682;
