Занятие №49. Дискретные случайные величины. Закон распределения дискретной случайной величины
№1. Найти ряд распределения случайной величины  -числа очков, выпадающих при одном бросании игральной кости.
-числа очков, выпадающих при одном бросании игральной кости.
Примечание: так как  –число очков, выпадающих при одном бросании игральной кости, то
–число очков, выпадающих при одном бросании игральной кости, то
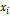
| ||||||
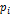
| 
| 
| 
| 
| 
| 
|
Стоит проверить:
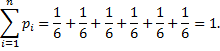
№2. Фермер содержит 15 коров, 5 из которых дают удои более чем по 4 500 литров молока в год. Случайным образом отобраны 3 принадлежащих фермеру коровы. Найти закон распределения случайной величины 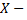 числа коров, дающих указанные высокие удои, среди отобранных.
числа коров, дающих указанные высокие удои, среди отобранных.
Примечание: случайная величина  может принимать значения: 0, 1, 2, 3.
может принимать значения: 0, 1, 2, 3.
Используя формулу Бернулли, можно найти соответствующие вероятности появления определенного количества коров из всех отобранных:
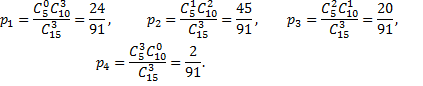
Записывают закон распределения в виде таблицы
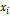
| ||||
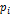
| 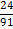
| 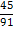
| 
| 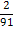
|
№3. Вероятность изготовления нестандартного изделия при налаженном технологическом процессе постоянна и равна 0,05. Для проверки качества изготавливаемых изделий отдел технического контроля берет из партии не более 4 изделий. Если будет обнаружено нестандартное изделие, то вся партия будет задержана. Найти ряд распределения случайной величины 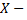 числа изделий, проверяемых ОТК из каждой партии.
числа изделий, проверяемых ОТК из каждой партии.
Примечание: пусть  проверяемое изделие стандартное;
проверяемое изделие стандартное; 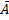 – проверяемое изделие нестандартное.
– проверяемое изделие нестандартное.
Согласно условию 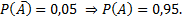
Следовательно 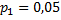 .
.
Если  т.е. если 1-е изделие стандартное, а 2-е нестандартное
т.е. если 1-е изделие стандартное, а 2-е нестандартное
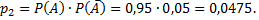
Аналогично можно найти
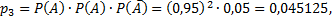
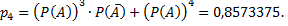
Контроль:
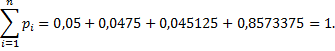
Искомый ряд распределения:
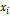
| ||||
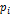
| 0,5 | 0,0475 | 0,045125 | 0,86 |
№4. Возможные значения случайной величины 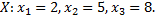 Известны вероятности последних двух возможных значений:
Известны вероятности последних двух возможных значений: 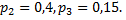 Найти вероятность
Найти вероятность 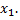
№5. Монета брошена 2 раза. Написать закон распределения случайной величины 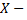 числа выпадений «герба».
числа выпадений «герба».
Примечание:

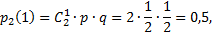
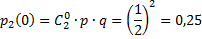
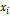
| |||
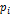
| 0,25 | 0,5 | 0,25 |
№6. Дискретная случайная величина 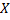 задана рядом распределения
задана рядом распределения
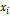
| -2 | |||
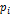
| 0,3 | 0,1 | 0,5 | 0,1 |
Найти 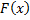 и построить ее график.
и построить ее график.
№7. Дискретная случайная величина 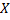 задана рядом распределения
задана рядом распределения
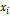
| |||
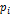
| 0,1 | 0,3 | 0,6 |
Найти 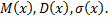
№8. Найти ряд распределения случайной величины 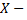 числа выпадений шестерки при 3-х бросаниях игральной кости. Вычислить
числа выпадений шестерки при 3-х бросаниях игральной кости. Вычислить 
Примечание: из данных задачи
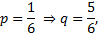

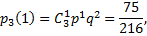
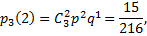
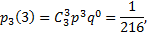
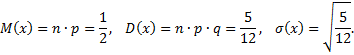
Дата добавления: 2015-08-11; просмотров: 3442;
