Теоремы сложения и умножения вероятностей. Примеры решения задач.

Задача №1. В урне 2 белых и 7 черных шаров. Из нее последовательно вынимают два шара. Какова вероятность того, что второй шар окажется белым при условии, что первый шар был черным?

Примечание: вынули один шар, следовательно, шаров осталось 8: 6 – черных и 2 – белых. По классическому определению вероятности можно легко найти интересующую нас вероятность события:

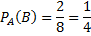
первый шар, который вынули из урны, оказался черным;

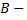второй шар, который вынули из урны, оказался белым.

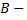Задача №2. В коробке находится 4 белых, 3 синих и 2 черных шара. Наудачу последовательно вынимают 3 шара. Какова вероятность того, что первый шар будет белым, второй – синим, а третий – черным? Примечание: следует обозначить события: вынули белый шар, вынули синий шар, 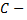вынули черный шар. Тогда

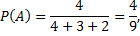
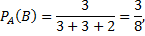
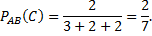
Если интересует вероятность одновременного появления этих событий, то следует применить теорему умножения

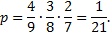
Задача №3. В урне 2 белых и 7 черных шаров. Из нее наудачу вынимают (без возврата) 2 шара. Какова вероятность того, что оба будут разных цветов?

Примечание: следует выделить события, вероятности которых необходимо найти:

вынули первый шар, и он оказался белым;

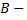вынули второй шар, и он оказался черным;

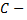вынули два шара, и они оказались разного цвета.

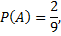
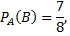
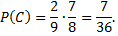
Задача №4. Три орудия стреляют в цель независимо друг от друга. Вероятность попадания в цель каждого равна 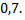Найти вероятность попадания в цель: а) только одного из орудий; б) хотя бы одного.

Примечание: a) выделим события: первое орудие попало в цель, два других не попали; 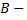второе орудие попало в цель, два других не попало; 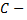третье орудие попало в цель, два других не попали; 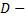одно орудие попало в цель.

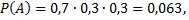
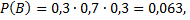
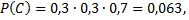
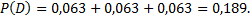
 б) 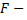хотя бы одно орудие попадет в цель, это значит, что либо одно орудие попадет, либо два орудия, либо три орудия попадут в цель.

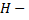два орудия попадут в цель; три орудия попадут в цель – выделены события, которые нас интересуют.

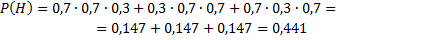
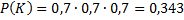
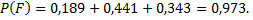
Задача №5. В первой коробке содержится 20 деталей, из них 18 стандартных; во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята деталь и переложена в первую. Найти вероятность того, что деталь, наудачу извлеченная из первой коробки, будет стандартной.

Примечание: пусть событие – из первой коробки извлечена стандартная деталь; – из второй коробки извлечена стандартная деталь; 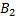– из второй коробки извлечена нестандартная деталь. Тогда

Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была положена стандартная деталь

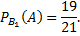
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была положена нестандартная деталь

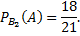
Тогда

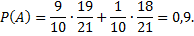
Задача №6. С первого автомата поступает на сборку 80% деталей, а со второго – 20%. На первом автомате брак составляет 1%, а на втором – 5%. Проверенная деталь оказалась бракованной. Что вероятнее: проверенная деталь изготовлена на первом автомате или на втором?

Примечание: пусть событие – проверенная деталь бракованная; 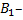проверенная деталь с первого автомата; 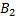– проверенная деталь со второго автомата. Таким образом,

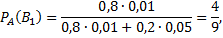
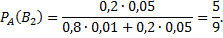
Другие примеры задач: 
- №7. Прибор содержит две микросхемы. Вероятность выхода из строя в течение 10 лет первой микросхемы равна 0,07, а второй – 0,10. Известно, что из строя вышла одна микросхема. Какова вероятность того, что из строя вышла первая микросхема?
- №8. Из 40 экзаменационных билетов студент Зайдуллин выучил 30. Каким выгоднее ему зайти на экзамен, первым или вторым?
- №9. Известно, что 90% изделий, выпускаемых данным предприятием, отвечает стандарту. Упрощенная схема проверки качества продукции признает пригодной стандартную деталь с вероятностью 0,96 и нестандартную с вероятностью 0,06. Определить вероятность того, что взятое наудачу изделие пройдет контроль.
- №10. С первого автомата поступает на сборку 80% деталей, а со второго – 20% таких же деталей. На первом автомате брак составляет 1%, а на втором – 5%. Проверенная деталь оказалась бракованной. Что вероятнее: эта деталь изготовлена на первом автомате или же она изготовлена на втором автомате?
- №11. В откормочный комплекс поступают телята из трех хозяйств. Из первого хозяйства телят поступает в 2 раза больше, чем из второго, а из первого – в 3 раза больше, чем из третьего. Первое хозяйство поставляет 15% телят, имеющих живой вес более 300 кг. Второе и третье хозяйства поставляют соответственно 25% и 35% телят, живой вес которых превышает 300 кг. Наудачу отобранный теленок при поступлении в откормочный комплекс весит 320 кг. Какова вероятность того, что он поступит из третьего хозяйства?