Занятие №44. Разложение функций в ряд Фурье
№1. Разложить функцию в ряд Фурье 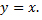
Примечание: функция 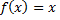 и ее производная
и ее производная 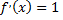 непрерывные функции на отрезке
непрерывные функции на отрезке 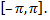 Ряд Фурье функции
Ряд Фурье функции  сходится на всей числовой прямой, причем в каждой точке
сходится на всей числовой прямой, причем в каждой точке 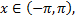 в которой
в которой  непрерывна, сумма ряда равна
непрерывна, сумма ряда равна 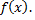 Следовательно функция может быть разложена в ряд Фурье. Так как она нечетная, то ее коэффициенты Фурье
Следовательно функция может быть разложена в ряд Фурье. Так как она нечетная, то ее коэффициенты Фурье 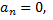
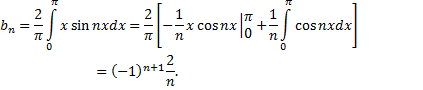
Таким образом, получаем ряд Фурье данной функции

В точках 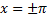 сумма ряда Фурье не совпадает со значениями функции
сумма ряда Фурье не совпадает со значениями функции 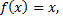 а равна
а равна
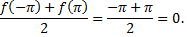
Вне отрезка 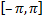 сумма ряда является периодическим продолжением функции
сумма ряда является периодическим продолжением функции 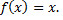
№2. Разложить функцию в ряд Фурье 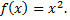
Примечание: функция 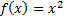 и ее производная
и ее производная  непрерывные функции на отрезке
непрерывные функции на отрезке 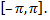 Ряд Фурье функции
Ряд Фурье функции  сходится на всей числовой прямой, причем в каждой точке
сходится на всей числовой прямой, причем в каждой точке 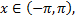 в которой
в которой  непрерывна, сумма ряда равна
непрерывна, сумма ряда равна 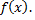 Следовательно функция может быть разложена в ряд Фурье. Так как функция четная, то ее коэффициенты Фурье
Следовательно функция может быть разложена в ряд Фурье. Так как функция четная, то ее коэффициенты Фурье 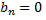


Значит, ряд Фурье данной функции имеет вид
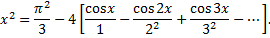
В точках  сумма ряда совпадает со значениями функции
сумма ряда совпадает со значениями функции 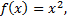 поскольку
поскольку
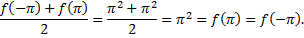
№3. Разложить в ряд Фурье функцию 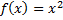 в заданном интервале в ряд синусов
в заданном интервале в ряд синусов
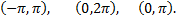
№4. Разложить в ряд Фурье периодическую функцию 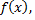 заданную на промежутке
заданную на промежутке  выражением
выражением
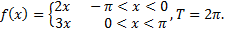
№5. Разложить в ряд Фурье периодическую функцию 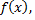 заданную на промежутке
заданную на промежутке 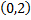 выражением
выражением
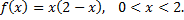
№6. Разложить в ряд Фурье периодическую функцию 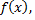 заданную на промежутке
заданную на промежутке 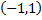 выражением
выражением
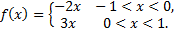
№7. Для функции 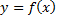 на заданном интервале вычислите коэффициенты Фурье
на заданном интервале вычислите коэффициенты Фурье 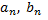
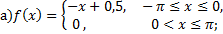
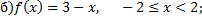
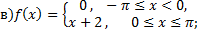
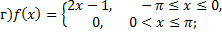
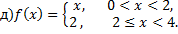
Дата добавления: 2015-08-11; просмотров: 1282;
