Занятие №45. Операции над множествами. Основные тождества алгебры множеств
№1. Докажите тождество 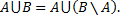
Примечание: чтобы доказать это тождество, нужно показать, что каждый элемент первого множества принадлежит второму и наоборот, т.е. эти множества совпадают.
Пусть  т.е.
т.е. 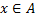 или
или 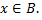 Если
Если 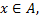 то
то 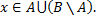 Если
Если 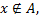 но
но 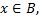 то
то 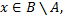 следовательно,
следовательно, 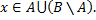
Пусть  т.е.
т.е. 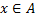 или
или 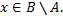 Если
Если 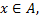 то
то 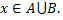 Если
Если 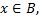 но
но
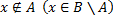 , то
, то 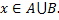
Таким образом, тождество доказано.
№2. Установите взаимно однозначное соответствие между всеми прямыми на плоскости и всеми точками координатной оси 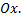
Примечание: зададим прямую двумя числами – точкой пересечения с осью 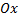

любое действительное число, в том числе может быть отрицательное, тогда вначале минус и углом наклона 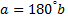 угол между прямой и положительным направлением оси
угол между прямой и положительным направлением оси 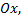 изменяется от
изменяется от 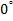 до
до 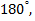 где
где  положительное действительное число из интервала
положительное действительное число из интервала 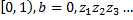
Сопоставим этим двум числам 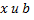 точку
точку 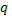 на оси
на оси 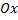 по следующему правилу:
по следующему правилу:

здесь знак числа 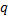 совпадает со знаком числа
совпадает со знаком числа  Видно, что по числу
Видно, что по числу 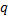 можно однозначно восстановить числа
можно однозначно восстановить числа 
Таким образом, мы установили однозначное соответствие между всеми прямыми на плоскости и всеми точками координатной оси 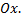
№3. Проверить, является ли отношением эквивалентности на множестве всех прямых на плоскости отношение «непересекающихся прямых».
Примечание: введем множество 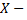 множество всех прямых на плоскости и отношение
множество всех прямых на плоскости и отношение
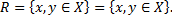
Это отношение будет отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Проверим наличие этих свойств.
 рефлексивно, так как для любой прямой
рефлексивно, так как для любой прямой 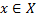 справедливо
справедливо  (считаем, что прямая параллельна самой себе).
(считаем, что прямая параллельна самой себе).
 симметрично, так как для любых прямых
симметрично, так как для любых прямых 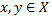 выполняется
выполняется 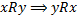 (так как если
(так как если  параллельна
параллельна 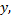 то и
то и  параллельна
параллельна  ).
).
 транзитивно, так как для любых прямых
транзитивно, так как для любых прямых 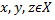 выполняется
выполняется 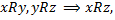 так как две прямые
так как две прямые  и
и 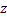 , параллельные третьей
, параллельные третьей 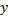 , параллельны.
, параллельны.
Таким образом, 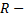 отношение эквивалентности.
отношение эквивалентности.
№4. Определите свойства следующих отношений:
1) «прямая 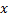 прямую
прямую 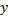 » на множестве прямых
» на множестве прямых
2) «число  больше числа
больше числа 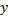 на 2» на множестве натуральных чисел
на 2» на множестве натуральных чисел
3) «число  делится на число
делится на число 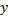 без остатка» на множестве натуральных чисел
без остатка» на множестве натуральных чисел
Примечание: 1. 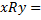 «прямая
«прямая  пересекает прямую
пересекает прямую 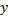 » на множестве прямых. Это отношение рефлексивно, так как «прямая
» на множестве прямых. Это отношение рефлексивно, так как «прямая  пересекает прямую
пересекает прямую  » выполняется для любой прямой (она пересекает себя в каждой точке); симметрическое, так как из того, что «прямая
» выполняется для любой прямой (она пересекает себя в каждой точке); симметрическое, так как из того, что «прямая  пересекает прямую
пересекает прямую 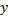 » следует, что «прямая
» следует, что «прямая  пересекает прямую
пересекает прямую  » для любых прямых
» для любых прямых 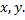
Также можно заметить, что это отношение не является тождественным, транзитивным и полным.
1. 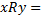 «число
«число  больше числа
больше числа  на 2» на множестве натуральных чисел. Это отношение антирефлексивное, так как ни для одного элемента из множества натуральных чисел не выполняется «число
на 2» на множестве натуральных чисел. Это отношение антирефлексивное, так как ни для одного элемента из множества натуральных чисел не выполняется «число  больше числа
больше числа  на 2»; антисимметрическое, так как для любых элементов
на 2»; антисимметрическое, так как для любых элементов 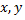 из множества натуральных чисел из того, что «число больше числа
из множества натуральных чисел из того, что «число больше числа  на 2» следует невыполнение того, что « число
на 2» следует невыполнение того, что « число  больше числа
больше числа  на 2».
на 2».
Также можно заметить, что это отношение не является тождественным, транзитивным и полным.
2. 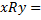 «число
«число  делится на число
делится на число  без остатка» на множестве натуральных чисел. Это отношение рефлексивно, так как для любого элемента
без остатка» на множестве натуральных чисел. Это отношение рефлексивно, так как для любого элемента  из множества натуральных чисел выполняется «число
из множества натуральных чисел выполняется «число  делится на число
делится на число  без остатка» и «число
без остатка» и «число  делится на число
делится на число  без остатка», следует, что
без остатка», следует, что 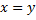 ; транзитивное, так как для любых элементов
; транзитивное, так как для любых элементов 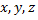 из множества натуральных чисел из того, что «число
из множества натуральных чисел из того, что «число  делится на число
делится на число 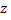 без остатка».
без остатка».
Также можно заметить, что это отношение не является симметрическим, антисимметрическим и полным. Это отношение является отношением порядка.
Дата добавления: 2015-08-11; просмотров: 1931;
