Занятие №43. Применение рядов к приближенным вычислениям
№1. Вычислить с точностью до 0,0001

Примечание: точное интегрирование здесь невозможно. Заменим  на
на 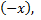 получим
получим

Умножая полученный ряд на 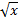
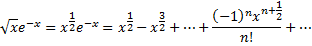
и почленно интегрируя в интервале  принадлежащем интервалу сходимости ряда
принадлежащем интервалу сходимости ряда 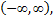 получим
получим
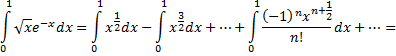
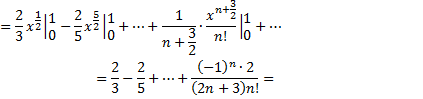

№2. Вычислите данный интеграл с помощью разложения подынтегральной функции в степенной ряд с точностью до 0,001:
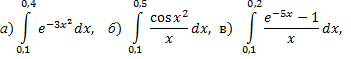
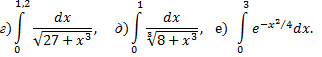
№3. Вычислить приближенно с точностью до 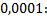
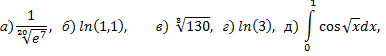

№3. Методом последовательного дифференцирования найти 5 первых членов, отличных от нуля, разложения в ряд решения уравнения
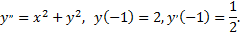
Примечание: будем искать решение уравнения в виде
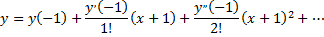
Найдем 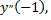 подставив
подставив 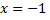 в исходное уравнение
в исходное уравнение 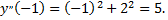 Для нахождения последующих коэффициентов дифференцируем заданное дифференциальное уравнение:
Для нахождения последующих коэффициентов дифференцируем заданное дифференциальное уравнение:
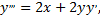




Подставляя найденные значения производных в искомый ряд, получим
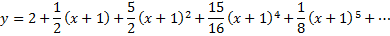
Дата добавления: 2015-08-11; просмотров: 1196;
