Абсолютная и условная сходимость знакопеременных рядов

Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.

Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся – в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.

Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.

Условно сходящиеся ряды такими свойствами не обладают. Возьмем, например, ряд

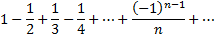
Переставим члены местами и сгруппируем их следующим образом

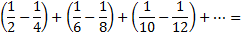
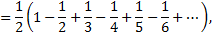
т.е. от перестановки членов ряда сумма его уменьшилась в 2 раза.

Рассмотрим пример. Исследовать сходимость ряда

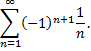
Это знакочередующийся ряд, для которого выполнены условия Лейбница. Следовательно, указанный ряд сходится. Однако ряд, составленный из модулей членов данного ряда, т.е.

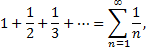
расходится (гармонический ряд). Такой ряд называют условно сходящимся.

Рассмотрим пример. Исследовать сходимость ряда

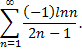
Так как члены знакочередующегося ряда, начиная со второго, убывают по абсолютной величине

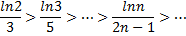
и предел общего члена

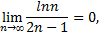
то по признаку Лейбница ряд сходится.

Ряд, составленный из абсолютных величин членов данного ряда,

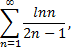
расходится, так как его члены больше членов расходящегося гармонического ряда, умноженного на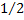

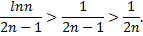
Следовательно, данный ряд условно сходящийся.

Рассмотрим пример. Исследовать сходимость ряда

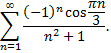
Ряд, составленный из абсолютных величин членов данного ряда, сходится, так как его члены меньше членов сходящегося обобщенно гармонического ряда при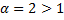

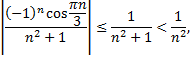
Следовательно, данный ряд сходится и притом абсолютно.

Контрольные вопросы

1. Какие ряды называют знакочередующимися?

2. Дать определение знакопеременного ряда.

3. Сформулировать признак Лейбница.

4. Какой ряд называют условно сходящимся?

5. Дать определение абсолютно сходящегося ряда.