Разложение правильной дроби
Теорема. Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей вида 1 – 4.
Пусть дробь 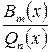 правильная. Разложим знаменатель дроби
правильная. Разложим знаменатель дроби 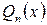 на множители. Найдем его корни, т. е. значения
на множители. Найдем его корни, т. е. значения 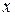 , при которых знаменатель обращается в нуль. Тогда многочлен
, при которых знаменатель обращается в нуль. Тогда многочлен 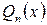 разложится на множители:
разложится на множители:
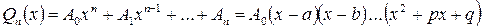 , где
, где
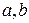 – действительные корни многочлена. Множитель
– действительные корни многочлена. Множитель 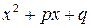 не разложим на линейные множители, т. к.
не разложим на линейные множители, т. к. 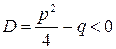 .
.
Вид элементарной дроби и число их в разложении определяется корнями знаменателя данной дроби. Каждому множителю знаменателя соответствует определенного вида дробь. Укажем, какому множителю какая дробь соответствует:
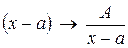
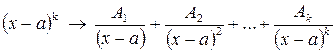
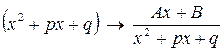 , если
, если 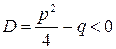 .
.
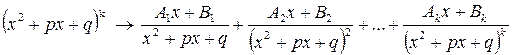 ,
,
если 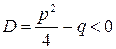 .
.
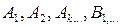 – пока неизвестные коэффициенты.
– пока неизвестные коэффициенты.
Разложить на простейшие дроби.
Пример 21. 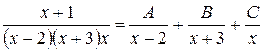 .
.
Пример 22. 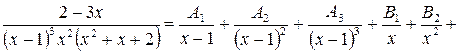
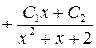
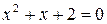 – не имеет действительных корней, т. к.
– не имеет действительных корней, т. к. 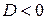 .
.
Пример 23. 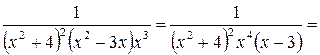
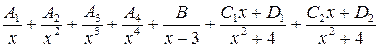 .
.
Пример 24. 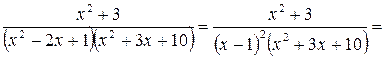
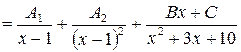 ,
,
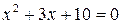 – не имеет действительных корней, т. к.
– не имеет действительных корней, т. к. 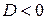 .
.
Дата добавления: 2015-08-11; просмотров: 1680;
