Из чертежа видно, что

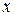пределы интегрирования

будут 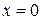и

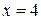
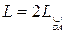(рис. 3).

Рис. 3 .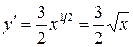

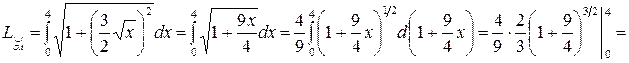
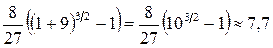
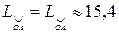(кв. ед.).

Пример 51. вычислить длину одной арки циклоиды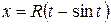

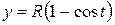(рис. 4).

Решение: Из соотношения 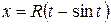видно, что значение 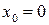соответствует ,

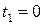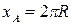соответствует ,

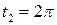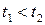. Так как уравнение линии

задано в декартовых координатах

(вид в), то используем формулу (2в),

табл.: , .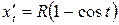

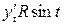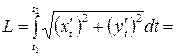Рис. 4

.

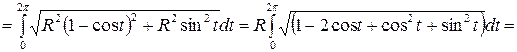
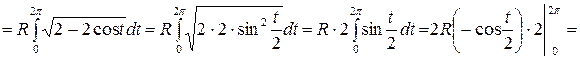
Пример 52. Вычислить длину кардиоиды ,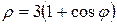

соответствующую .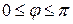

Решение: Уравнение кривой задано в полярных координатах, следовательно, при решении воспользуемся формулой (2д). Изменение задано, следовательно, выполнение чертежа необязательно.

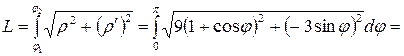
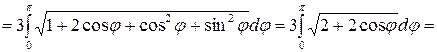
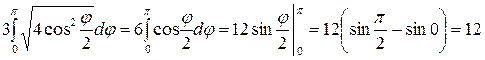(ед. длины).

Пример 53. Вычислить объем тела, образованного вращением вокруг оси 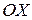фигуры, ограниченной параболой 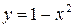и осью 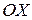(рис. 5).

Решение: Парабола 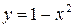расположена ветвями вниз, вершина находится в точке 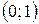, и ось 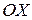пересекает в точках 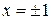. Для решения воспользуемся формулой (3а), табл.

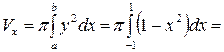
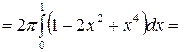
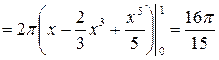(куб. ед.).

Рис. 5

Пример 54. Вычислить объем тела, образованного вращением гиперболы 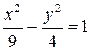, отсеченной прямыми 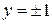, вокруг оси 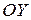(рис. 6).

Решение: Для решения задачи воспользуемся формулой (3б), табл.

; ,

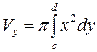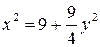находим из уравнения параболы:

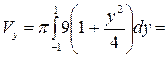
Рис. 6 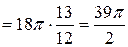(куб. ед.).

Замечание: Иногда при решении задач полезно использовать рекуррентную формулу:

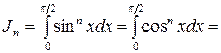
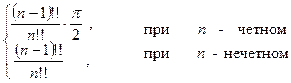
Знак (двойной факториал) означает произведение целых чисел, начиная с 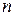, через одно с убыванием. Например, 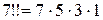(только нечетные множители).