Интегрирование методом замены переменной. Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т.е. перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной.
В приложениях важное значение имеют интегралы
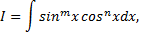
где 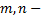 целые неотрицательные числа.
целые неотрицательные числа.
Различают два случая:
1) хотя бы один из показателей  или
или  есть число нечетное;
есть число нечетное;
2) оба показателя  и
и 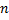 есть числа четные.
есть числа четные.
В первом случае интеграл 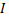 берется непосредственно.
берется непосредственно.
Рассмотрим пример. Найти
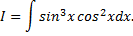
Последовательно полагаем
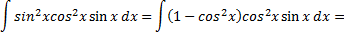
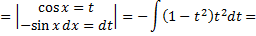
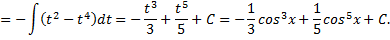
Во втором случае для вычисления интеграла 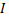 используют формулы двойного аргумента
используют формулы двойного аргумента
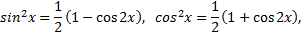
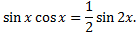
Рассмотрим пример. Найти

Имеем
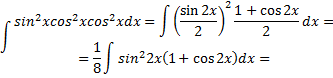
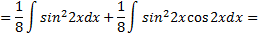
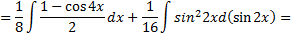

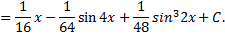
Важное значение имеют интегралы вида

Данные интегралы вычисляются на основании формул тригонометрии:
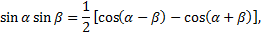

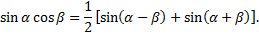
Рассмотрим пример. Найти
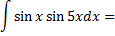
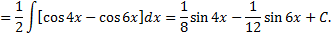
Дата добавления: 2015-08-11; просмотров: 891;
