Интегрирование элементарных дробей
Важный класс функций, интегралы от которых всегда выражаются через элементарные функции, образуют рациональные функции, которые можно представить в виде дроби
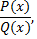
где 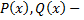 многочлены.
многочлены.
Если степень многочлена в числителе равна или больше степени многочлена в знаменателе, то, выполнив деление, получим
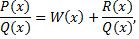
где 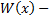 многочлен,
многочлен, 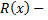 многочлен степени ниже, чем
многочлен степени ниже, чем 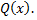
Рассмотрим пример:
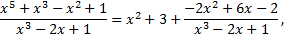

Если рациональная функция
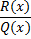
имеет степень многочлена в числителе меньше степени многочлена в знаменателе, то рациональная дробь называется правильной и ее можно разложить на элементарные дроби, если она не является таковой.
Простейшей или элементарной дробью называется дробь одного из следующих четырех типов
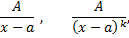
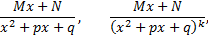
где 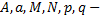 постоянные числа;
постоянные числа;  целое,
целое,
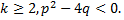
Многочлен может быть представлен в виде произведения

где  коэффициент при старшей степени многочлена
коэффициент при старшей степени многочлена 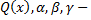 корни уравнения
корни уравнения 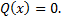 Множители
Множители
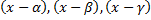
называются элементарными множителями.
Таким образом, рациональную функцию
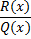
можно представить в виде
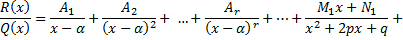
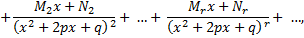
где 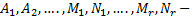 некоторые вещественные числа.
некоторые вещественные числа.
Чтобы определить числа 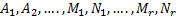 умножим обе части разложения на
умножим обе части разложения на 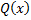 . Равенство между многочленом
. Равенство между многочленом 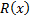 и многочленом, который получится в правой части, должно быть справедливо для всех
и многочленом, который получится в правой части, должно быть справедливо для всех  , тогда и коэффициенты, стоящие при равных степенях
, тогда и коэффициенты, стоящие при равных степенях  , должны быть равны между собой. Приравнивая их, получим систему уравнений первой степени, из которой найдем неизвестные числа
, должны быть равны между собой. Приравнивая их, получим систему уравнений первой степени, из которой найдем неизвестные числа 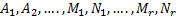 .
.
Такой метод отыскания коэффициентов разложения рациональной функции называется методом неопределенных коэффициентов.
Рассмотрим пример.
Разложим рациональную функцию
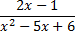
на элементарные дроби.
Разложим на множители знаменатель, используя формулу разложения на множители квадратного трехчлена
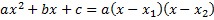 ,
,
где 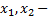 корни соответствующего однородного квадратного уравнения.
корни соответствующего однородного квадратного уравнения.
Разложим квадратный трехчлен на множители
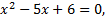
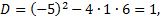

следовательно

тогда
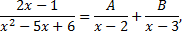
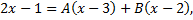
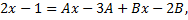
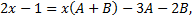
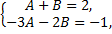
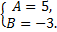
Таким образом,
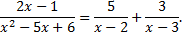
Рассмотрим пример.
Найти разложение рациональной функции
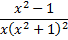
на элементарные дроби.
Воспользуемся выше предложенной формулой разложения, получим
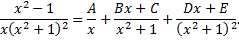
Умножим обе части равенства на 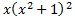 в результате, получим
в результате, получим

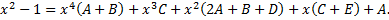
Составим систему, решая ее, найдем неизвестные 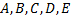
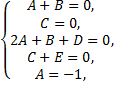
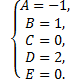
Искомое разложение имеет вид
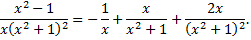
Дата добавления: 2015-08-11; просмотров: 1188;
