Интегрирование функций, содержащих квадратный трехчлен

На практике часто встречаются интегралы следующего вида

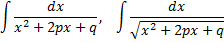
или

где многочлен 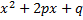не имеет вещественных корней, так что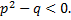

Для того, чтобы привести интегралы такого вида к табличным, необходимо из трехчлена в знаменателе выделить полный квадрат

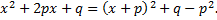
Это представление подсказывает подстановку 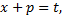откуда 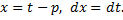Положим далее 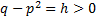и перейдем к переменной 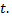В результате интеграл

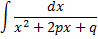
преобразуется к виду

Если 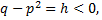то интеграл преобразуется к виду

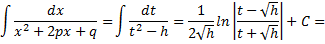
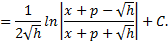
Интеграл

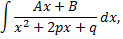
где многочлен 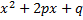не имеет вещественных корней, так что 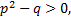преобразуется к виду

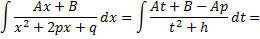
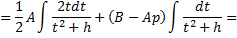
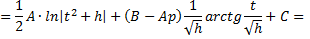
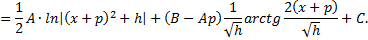
Если 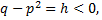то интеграл преобразуется к виду

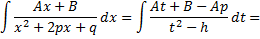
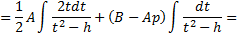
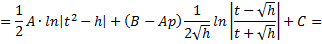
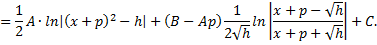
Рассмотрим пример. Вычислить интеграл

Выделим в знаменателе полный квадрат

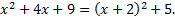
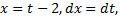Сделаем подстановку откуда поэтому

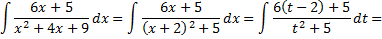
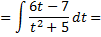
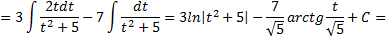
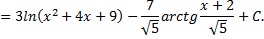
Рассмотрим пример. Вычислить интеграл

Выделим в знаменателе полный квадрат

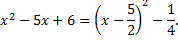
Сделаем подстановку

Тогда

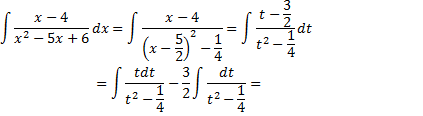
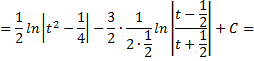
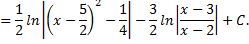
Рассмотрим пример. Вычислить интеграл

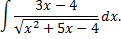
Выделим в знаменателе полный квадрат

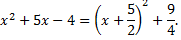
Сделаем подстановку

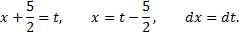
Тогда

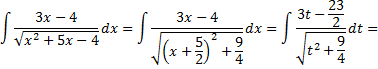
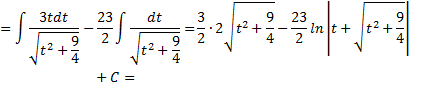
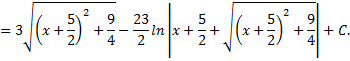
Контрольные вопросы

1. По какой формуле осуществляется интегрирование по частям?

2. В каких случаях применяют метод интегрирования по частям?

3. Как привести интегралы, содержащие квадратный трехчлен к табличным интегралам?

4. К каким табличным интегралам чаще всего приводят интегралы, содержащие квадратный трехчлен?