Интегрирование дифференциальных уравнений
Степенные ряды могут применяться для нахождения приближенного решения дифференциального уравнения, если его решение не удается найти в элементарных функциях.
Пример. Найти решение дифференциального уравнения
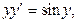
удовлетворяющее начальному условию 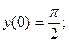
Решение. Уравнение допускает разделение переменных :
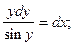
однако интеграл от левой части уравнения не выражается в элементарных функциях. Будем искать решение в виде ряда Маклорена
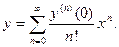
Так как 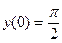 , а
, а 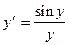 (*) то
(*) то 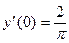 .
.
Дифференцируя по х обе части равенства (*), находим
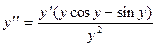 ; (**)
; (**)
откуда
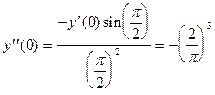 ;
;
Дифференцируя обе части равенства (**) , находим 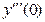 . Продолжая этот процесс, можно получить любое число членов разложения в ряд Маклорена искомого решения
. Продолжая этот процесс, можно получить любое число членов разложения в ряд Маклорена искомого решения
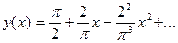
Дата добавления: 2015-08-11; просмотров: 721;
