Приближенное вычисление значений функций.
Для нахождения приближенного значения функции f(x) в точке 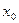
с заданной точностью поступим следующим образом. Разложим функцию f(x) в ряд по степеням 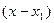 с интервалом сходимости, содержащим точку
с интервалом сходимости, содержащим точку 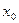 , где
, где 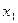 - точка , в которой значение функции и ее производных вычисляются легко и точно. Переменной х придадим значение
- точка , в которой значение функции и ее производных вычисляются легко и точно. Переменной х придадим значение 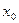 и в полученном числовом ряду
и в полученном числовом ряду 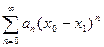 оставим только члены, гарантирующие только заданную точность вычислений. Минимаьное число
оставим только члены, гарантирующие только заданную точность вычислений. Минимаьное число 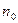 таких членов определим из соответствующей оценки либо остатка формулы Тейлора , либо остатка ряда.
таких членов определим из соответствующей оценки либо остатка формулы Тейлора , либо остатка ряда.
Пример. Вычислить с точностью 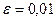 число е.
число е.
Решение. Так как
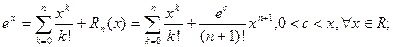
то из оценки
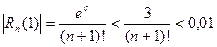
следует, что 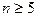 , т.е. необходимо взять пять слагаемых .
, т.е. необходимо взять пять слагаемых .
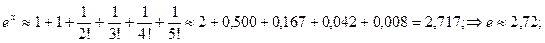
Пример 2. Вычислить 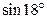 с точностью 0,0001.
с точностью 0,0001.
Решение так как  и ряд
и ряд
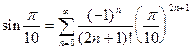
является рядом Лейбница, то из оценки
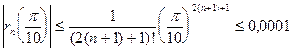
получаем 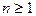 . Таким образом
. Таким образом
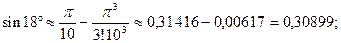
Дата добавления: 2015-08-11; просмотров: 1016;
