Ортонормированные системы.
Определение: Евклидовым пространством называют линейное пространство L, в котором задано скалярное умножение, т.е. отображение f:L®R, ставящее упорядоченной паре элементов пространства L в соответствие число и удовлетворяющее аксиомам скалярного умножения :
1.(x,y)=(y,x), x,yÎL;
2.(x+y,z)=(x,z)+(y,z), x,y,zÎL;
3.( 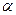 x,y)=
x,y)= 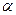 (x,y), x,y
(x,y), x,y 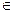 L, aÎR;
L, aÎR;
4.(x,x)³0, и (x,x)=0 Û x=0.
Определение: Линейное (евклидово) пространство бесконечномерное, если в нем можно выбрать любое количество линейно независимых элементов.
Определение: Функция называется кусочно -непрерывной на отрезке [a;b], если она непрерывна всюду на отрезке [a;b] за исключением конечного числа точек, в которых эта функция имеет разрывы первого рода.
Множество всех кусочно-непрерывных на [a;b] функций образует линейное пространство. При этом под сложением элементов линейного пространства и умножением элемента на число понимают обычные операции сложения функций и умножения функции на число. Нулевым элементом в этом линейном пространстве является функция, тождественно равная нулю.
Произведение любых двух функций f и g из рассматриваемого линейного пространства является кусочно-непрерывной функцией, и, следовательно, интегрируемой на отрезке [a;b] функцией. Значит в этом линейном пространстве определено отображение, которое любым двум функциям f и g ставит в соответствие действительное число (f,g):
(f, g)= 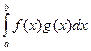 (1)
(1)
Формула (1) задает скалярное умножение в рассматриваемом линейном векторном пространстве кусочно-непрерывных функций.
Легко проверить, что данное отображение удовлетворяет первым трем аксиомам скалярного умножения. Аксиома (4) не выполняется, действительно:
(f, f)= 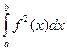 =0
=0
Для любой функции f(x), равной нулю на [a;b] всюду, кроме некоторого конечного числа точек. Такая функция кусочно-непрерывна на [a; b], но не является нулевым элементом линейного пространства, т.к. она не равна тождественно нулю на всем отрезке [a; b] .
Чтобы четвертая аксиома скалярного умножения для введенного отображения выполнялась, будем рассматривать только те кусочно-непрерывные на отрезке [a;b] функции f(x), значения которых в каждой внутренней точке их разрыва 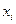 равны полусумме правого и левого пределов в этой точке:
равны полусумме правого и левого пределов в этой точке:

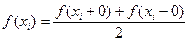 (2)
(2)
Значения на границах отрезка [a;b] одинаковы и равны полусумме односторонних пределов функции в этих точках:
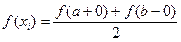 (3)
(3)
Докажем, что для суженного линейного пространства кусочно-непрерывных функций введенное отображение (f,g) удовлетворяет аксиоме (4) скалярного умножения.
Пусть (f,f)= 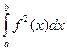 =0 и точка
=0 и точка 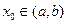 -произвольная точка непрерывности функции f, в которой f(
-произвольная точка непрерывности функции f, в которой f( 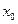 )
) 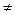 0. Тогда
0. Тогда 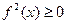 на [a,b],
на [a,b], 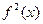 непрерывна в
непрерывна в 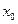 и
и 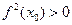 .
.
По свойствам определенного интеграла 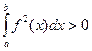 , что противоречит предположениям.
, что противоречит предположениям.
Следовательно, в любой точке x непрерывности функции f выполняется равенство f(x)=0.
Пусть теперь 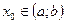 -точка разрыва функции f(x). Т.к. точек разрыва у функции конечное число, то для любой точки разрыва найдется ее проколотая окрестность, в которой функция f(x), будет непрерывна и, значит, равна нулю. Поэтому
-точка разрыва функции f(x). Т.к. точек разрыва у функции конечное число, то для любой точки разрыва найдется ее проколотая окрестность, в которой функция f(x), будет непрерывна и, значит, равна нулю. Поэтому
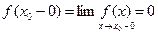 ,
, 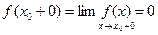 ,
,
т.к. f(x)=0 в точках непрерывности. Тогда, согласно условию (2), имеем равенство 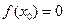 . Аналогично для точек a и b найдутся интервалы, в которых функция f(x) непрерывна. Следовательно, f(a+0)=0 и f(b-0)=0. В силу (3) получаем f(a)=f(b)=0.
. Аналогично для точек a и b найдутся интервалы, в которых функция f(x) непрерывна. Следовательно, f(a+0)=0 и f(b-0)=0. В силу (3) получаем f(a)=f(b)=0.
Т.е.линейное пространство всех кусочно-непрерывных на отрезке [a,b] функций, удовлетворяющих условиям (2) и (3), является евклидовым пространством со скалярным произведением (1).
Определение: Неотрицательное число:
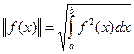 ,
,
называется нормой функции f(x) в евклидовом пространстве. Учитывая, что
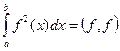 ,
,
то норму функции можно записать в виде: 
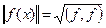 .
.
Функция называется нормированной, если ее норма равна 1.
Определение: Две функции f(x) и g(x) называются ортогональными на [a,b], если их скалярное произведение равно нулю, т.е.
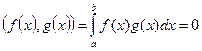
Пример: Функции f(x)=x и g(x)= 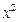 являются ортогональными на отрезке [-1,1].
являются ортогональными на отрезке [-1,1].
Вычислим скалярное произведение:
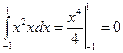 .
.
Пусть в евклидовом пространстве задана некоторая бесконечная последовательность элементов 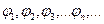 Эту последовательность называют ортонормированной системой, если для любых натуральных i и j,
Эту последовательность называют ортонормированной системой, если для любых натуральных i и j,
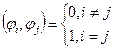 ,
,
т.е. элементы этой последовательности попарно ортогональны и все имеют единичную норму.
Дата добавления: 2015-08-11; просмотров: 1173;
