Ряды Фурье по ортогональным системам функций

Определение: Пусть 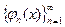ортогональная система функций.

Выражение вида: 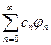(1) называется обобщенным рядом Фурье по ортогональной системе функций .

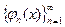Если 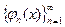-основная тригонометрическая система функций, ряд называется тригонометрическим рядом Фурье.

Пусть f(x)- кусочно-непрерывная, принадлежащая евклидовому пространству на [a,b]. И пусть имеет место разложение:

,

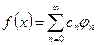умножим обе части этого выражения на 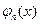и проинтегрируем на [a,b].

Так как система функций 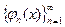-ортогональна, то все интегралы в правой части равны нулю, кроме одного, когда индексы совпадают. Следовательно:

,

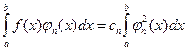или исходя из определений

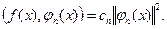
Мы можем выразить коэффициенты обобщенного ряда Фурье:

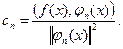(2)

Тогда обобщенный ряд Фурье функции f(x),принадлежащей евклидовому пространству на [a,b] по системе ортогональных функций имеет вид:

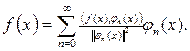(3)

Мы формально записали разложение функции в обобщенный ряд Фурье. Вопрос о сходимости этого ряда остается открытым.