Неравенство Бесселя и его следствия.

Для ряда Фурье (1) элемента f определим n-ю частичную сумму

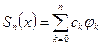
Определение: Обобщенный ряд Фурье (1) называется сходящимся по норме к элементу g евклидового пространства, если

.

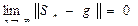Величина 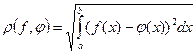называется средним квадратичным отклонением функций. .

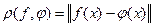Теорема: Из всех обобщенных многочленов вида 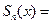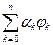, 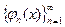ортонормированная система функций, n-я частичная сумма ряда Фурье осуществляет наилучшее приближение элемента f в смысле нормы, порождаемой скалярным произведением эвклидова пространства.

(т.е. является наилучшей средней квадратичной аппроксимацией функции f(x) на [a,b].

Значит при заданных f(x) и n среднее квадратичное отклонение минимально, когда .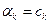

Для доказательства рассмотрим квадрат нормы:

.

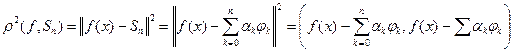Т.к. 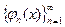-ортонормированная система функций, то

= +

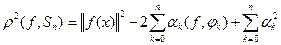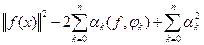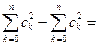
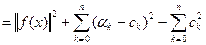
Первое и третье слагаемые не зависят от 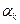,отсюда следует, что минимальное значение достигается, когда второе слагаемое равно нулю, при .

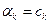Для коэффициентов Фурье справедлива следующая

Теорема: Для любого элемента f(x) и любой ортонормированной системы 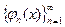ряд (составленный из квадратов коэффициентов Фурье функции f(x)) сходится и справедливо неравенство Бесселя: .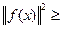

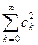Замечание: если 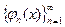ортогональная, но не нормированная система функций, то неравенство Бесселя принимает вид: .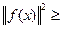

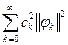Из предыдущей теоремы следует, что .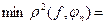

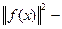
Но левая часть равенства больше или равна нулю, следовательно:

,

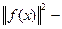
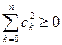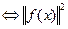
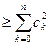
Следовательно, все частичные суммы знакоположительного ряда 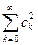ограничены одним и тем же числом 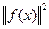, и следовательно ряд сходится.

Переходя в последнем неравенстве к пределу при 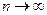,получим неравенство Бесселя.

Определение: Ряд Фурье называется равномерно сходящимся к функции f(x) на [a,b], если последовательность его частичных сумм сходится к f(x) равномерно, т.е.

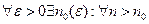и .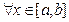

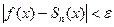Замечание: Из определения равномерной сходимости следует

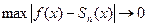при .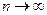

Теорема: Если обобщенный ряд Фурье функции f(x) 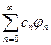сходится к этой функции на [a,b] равномерно, то он сходится к f(x) на [a,b] и в среднем квадратичном.

Доказательство: Пусть ряд Фурье 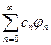функции f(x) сходится к ней на [a,b] равномерно, т.е.

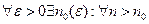и .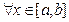

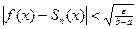Тогда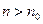

Следовательно, 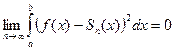и ряд Фурье по определению сходится к f(x) и в среднем квадратичном.

Определение: В бесконечномерном евклидовом пространстве ортонормированную систему 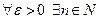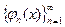называют замкнутой, если для любого элемента f этого пространства

и числа ,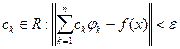

т.е. сходится в среднем квадратичном.

Теорема: Для того, чтобы обобщенный ряд Фурье 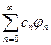функции f(x) сходился к f(x) на [a,b] в среднем квадратичном необходимо и достаточно, чтобы неравенство Бесселя обращалось в равенство Парсеваля- Стеклова .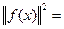

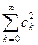Эту теорему можно сформулировать иначе:

Если ортонормированная система 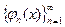замкнута в евклидовом пространстве на [a,b], то для любого элемента этого пространства f(x) верно равенство Парсеваля- Стеклова .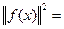

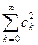Необходимость: Пусть 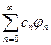сходится к f(x) на [a,b] в среднем квадратичном, т.е.

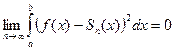, по теореме об экстремальном свойстве коэффициентов Фурье

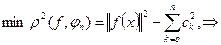
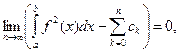
тогда

.

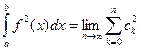
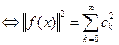Достаточность: Пусть выполняется равенство Парсеваля-Стеклова

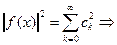
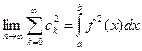
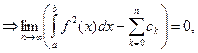
тогда

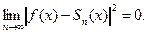
Следовательно, обобщенный ряд Фурье сходится к f(x) на [a,b] в среднем квадратичном.

Определение: В бесконечномерном евклидовом пространстве ортогональную систему функций 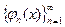называют полной, если единственным элементом в этом пространстве ортогональным всем элементам 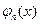этой системы является нулевой элемент.

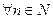
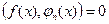следовательно .

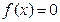Теорема

Любая замкнутая ортогональная система функций 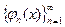бесконечномерного эвклидова пространства является полной.

Доказательство

Пусть 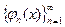- замкнутая ортогональная система функций и для 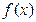выполняется условие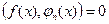 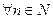. Тогда коэффициенты Фурье равны нулю.

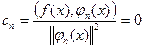. Так как система замкнута, то выполняется равенство Парсеваля-Стеклова. 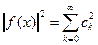, а значит и левая часть равенства равна нулю. 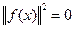, а следовательно, и 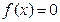, а система функций 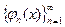является полной.

Преобразуем равенство Парсеваля-Стеклова с учётом традиционных обозначений коэффициентов тригонометрического ряда Фурье:

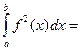
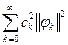
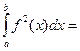
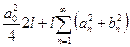, или 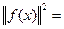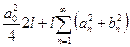- уравнение Ляпунова.

Основная тригонометрическая система функций обладает полнотой, то есть для любой функции интегрируемой с квадратом имеет место равенство Парсеваля-Стеклова, следовательно функцию 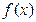с периодом 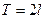можно разложить в ряд Фурье, который будет сходиться к функции 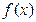в среднем квадратичном.