Комплексная форма тригонометрического ряда Фурье

Тригонометрический ряд Фурье имеет вид

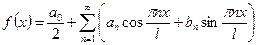
Используя формулы Эйлера

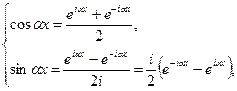
получаем

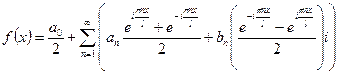
Сгруппируем коэффициенты при одинаковых экспонентах:

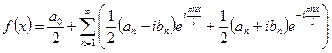
полагая,

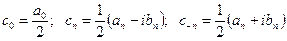
Получим

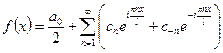
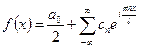. (1)

Это и есть комплексная форма тригонометрического ряда Фурье.

Найдём коэффициенты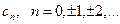

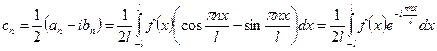, (2)

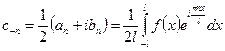. (3)

Эти выражения можно объединить в одну формулу, добавив n=0

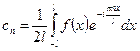, (4)

где n=0, ±1, ±2, ±3,…

Выражения 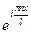называют гармониками. Числа 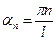n=0, ±1, ±2, ±3,… - волновые числа функции. Множество всех волновых чисел – спектр. Коэффициенты 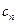- комплексные амплитуды.