Непрерывность интеграла как функции параметра

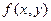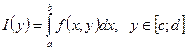Теорема. Пусть функция непрерывна в прямоугольнике и . Тогда функция непрерывна на отрезке .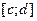

Зафиксируем произвольное 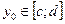. В предыдущем параграфе было доказано, что

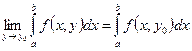, в других обозначениях это означает

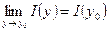
Следовательно, функция 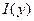непрерывна в точке .

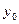Замечание 1. Условие непрерывности функции 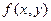в прямоугольнике является достаточным для непрерывности 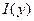на отрезке .

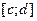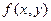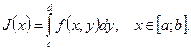Замечание 2. Аналогично можно доказать утверждение: Если функция непрерывна в прямоугольнике и Тогда функция 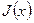непрерывна на отрезке .

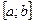Следствие. Если функция 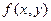непрерывна в прямоугольнике , то одновременно непрерывны функции 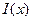на отрезке 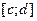и 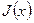непрерывна на отрезке 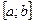. Тогда одновременно существуют интегралы

,

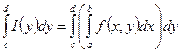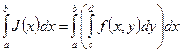
Эти интегралы называются повторными.