Пределы интегрирования, зависящие от параметра
Пусть функция 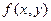 определена в плоской области (S), ограниченной линиями y=c, y=d (c<d) и
определена в плоской области (S), ограниченной линиями y=c, y=d (c<d) и 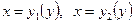 , где
, где 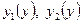 - функции, непрерывные на отрезке
- функции, непрерывные на отрезке 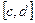 .
.
При каждом фиксированном 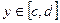 существует
существует 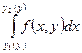 . Каждому значению
. Каждому значению 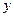 будет соответствовать определенное значение интеграла. Следовательно,
будет соответствовать определенное значение интеграла. Следовательно, 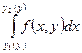 является функцией переменной (параметра)
является функцией переменной (параметра) 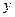 , определенной на отрезке
, определенной на отрезке 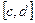 . Введем обозначения:
. Введем обозначения:
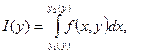
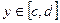 (1)
(1)
Примем без доказательства два утверждения.
Теорема 1. Пусть функция 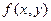 непрерывна в плоской области (S) и
непрерывна в плоской области (S) и 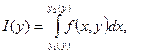
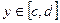 . Тогда функция
. Тогда функция 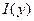 непрерывна на отрезке
непрерывна на отрезке 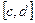 .
.
Теорема 2.Пусть функция 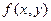 непрерывна в плоской области (S) и имеет на ней непрерывную частную производную
непрерывна в плоской области (S) и имеет на ней непрерывную частную производную 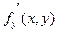 . Пусть функции
. Пусть функции 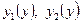 определены на отрезке
определены на отрезке 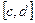 и имеют на нем непрерывные производные
и имеют на нем непрерывные производные  . Пусть
. Пусть 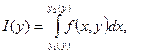
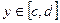 . Тогда для любого
. Тогда для любого 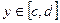 существует
существует 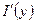 , причем
, причем
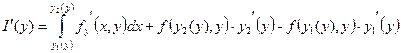
ПримерДан интеграл 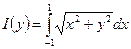 . Найти
. Найти 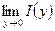 .
.
Подынтегральная функция 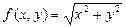 непрерывна на всей плоскости Оху, следовательно, будет непрерывна в любом прямоугольнике
непрерывна на всей плоскости Оху, следовательно, будет непрерывна в любом прямоугольнике 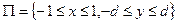 , где
, где 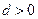 . По теореме из §2 возможен предельный переход по параметру под знаком интеграла
. По теореме из §2 возможен предельный переход по параметру под знаком интеграла
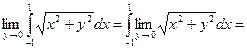
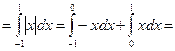
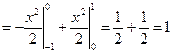 .
.
Дата добавления: 2015-08-11; просмотров: 638;
