Дифференцирование интегралов по параметру
Теорема. Пусть функция 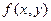 непрерывна в прямоугольнике
непрерывна в прямоугольнике  и имеет в нем непрерывную частную производную
и имеет в нем непрерывную частную производную 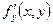 . Пусть
. Пусть 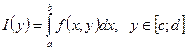 .
.
Тогда:
- функция
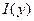 имеет на отрезке
имеет на отрезке 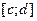 производную
производную 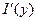 ;
; -
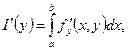 т.е.
т.е. 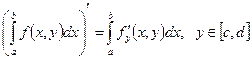 ;
; -
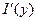 непрерывна на отрезке
непрерывна на отрезке 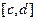 .
.
Доказательство. Зафиксируем произвольную точку 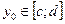 . Дадим приращение
. Дадим приращение 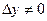 таким образом, чтобы
таким образом, чтобы 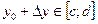 . Вычислим значение функции
. Вычислим значение функции 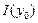 и
и  :
:
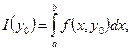
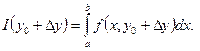
Найдем отношение приращения функции к приращению аргумента:
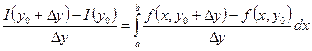 (1)
(1)
Согласно теореме Лагранжа
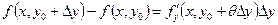 ,
,
где 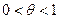 . Тогда
. Тогда
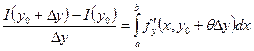 . (2)
. (2)
По условию теоремы частная производная 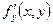 непрерывна. Перейдем в соотношении (2) к пределу при
непрерывна. Перейдем в соотношении (2) к пределу при 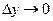 . Учитывая теорему о предельном переходе под знаком интеграла, получаем
. Учитывая теорему о предельном переходе под знаком интеграла, получаем
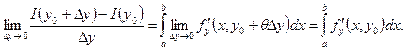
Следовательно, 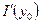 существует и
существует и 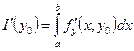 . В силу произвольности
. В силу произвольности 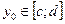 , делаем вывод о том, что
, делаем вывод о том, что 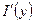 существует на всем отрезке
существует на всем отрезке 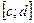 , кроме того,
, кроме того,
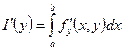 . (3)
. (3)
По условию теоремы 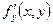 непрерывна, тогда из соотношения (3) и теоремы о непрерывности интеграла как функции параметра следует непрерывность
непрерывна, тогда из соотношения (3) и теоремы о непрерывности интеграла как функции параметра следует непрерывность 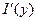 на отрезке
на отрезке 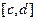 .
.
Дата добавления: 2015-08-11; просмотров: 1035;
