Вычисление тройных интегралов

Пусть 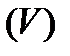- прямоугольный параллелепипед 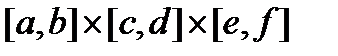(рис.2), который проектируется на YOZ в прямоугольник 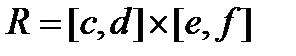. Для такого 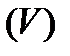имеет место теорема.

Теорема 2. Если для функции 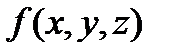существует тройной интеграл 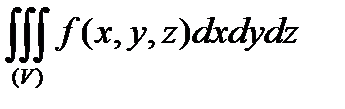и для любого фиксированного 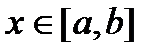существует двойной интеграл

,

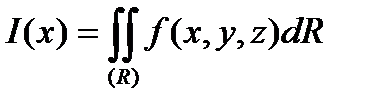то существует и повторный интеграл:

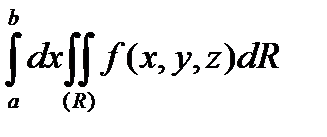
и

.

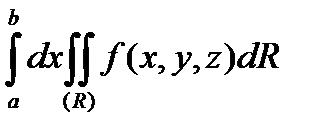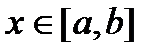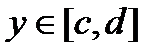Если дальше предположить, что для любых і существует интеграл 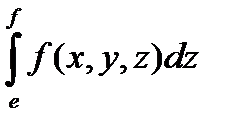, то

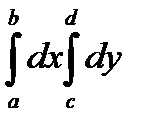
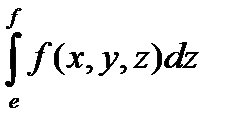. (1)

При нужном существовании интегралов переменные интегрирования в формуле (1) можно менять местами.

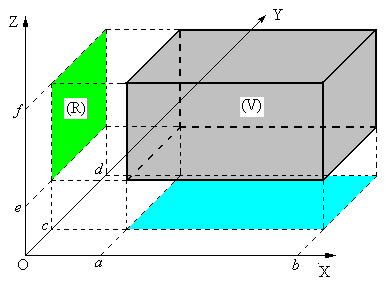
Рис.2.

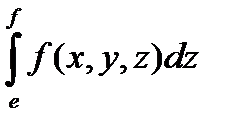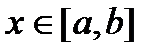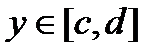Замечание. Можно показать, что если существует тройной интеграл и интеграл для любых и , то

,

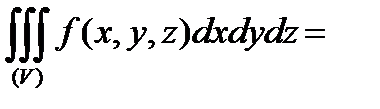
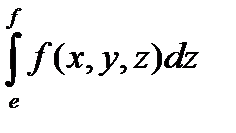де .

Пусть 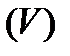имеет произвольную форму, функция 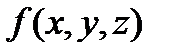определена на 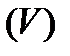. Построим 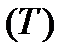- прямоугольный параллелепипед, который содержит в себе 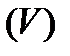, и определим на нем функцию :

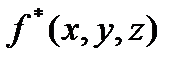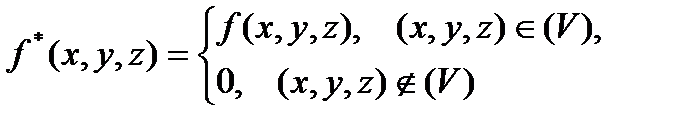
Этим путем получаются все следующие формулы.

Пусть тело 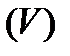находится между плоскостями 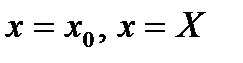(рис.3), и каждой плоскостю 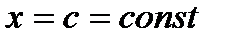, перпендикулярной оси ОХ, где 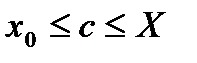, пересекается по некоторой фигуре с площадью 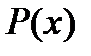, проекцию которой на плоскость YOZ обозначим 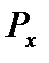(рис.3).

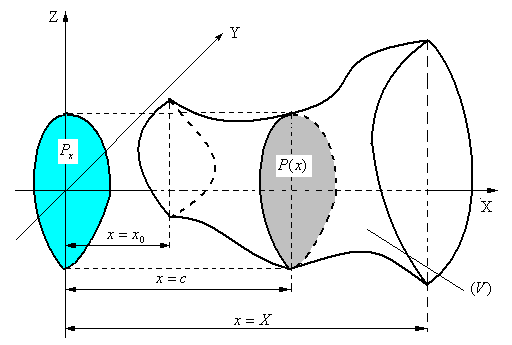
Рис.3

Тогда

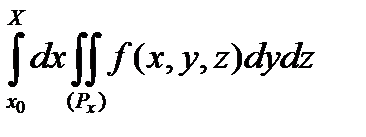(2)

в предположении существования двойного и тройного интегралов.

Пусть 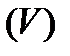- цилиндрический брус с образующей, параллельной оси OZ, ограниченный снизу и сверху соответственно поверхностями (рис.4):

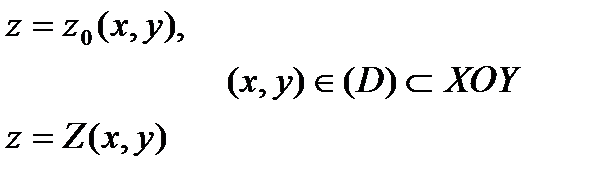
Тогда аналогично (2) имеем:

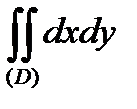
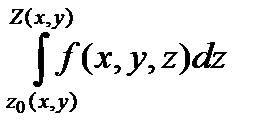, (3)

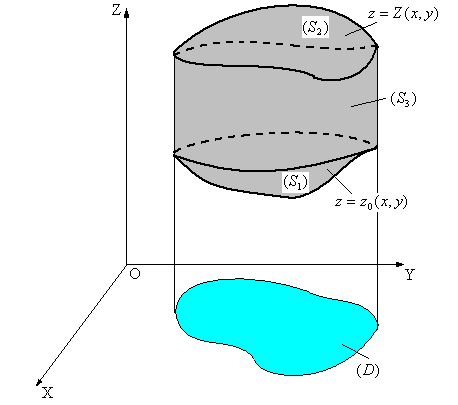
Рис.4.

если предположить существование тройного и простого интегралов.

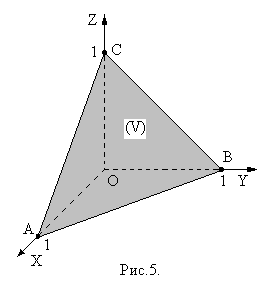Пример. Вычислить 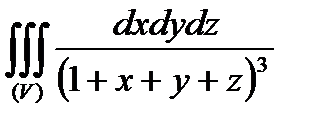, где область 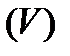определяется следующим образом (рис.5):

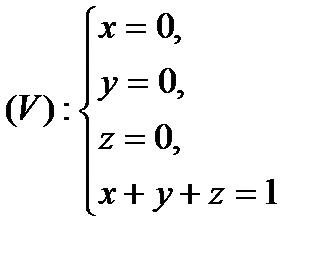
Тогда

.