Определение тройного интеграла
Лекция 48. Тройной интеграл и его вычисление
План
- Определение тройного интеграла
- Свойства интегрируемых функций и тройных интегралов
- Вычисление тройных интегралов
Определение тройного интеграла
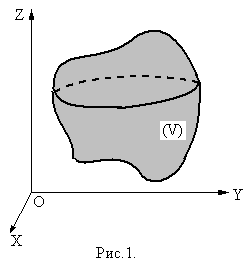
Пусть в некоторой пространственной области 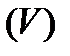 (рис.1) определена функция:
(рис.1) определена функция:
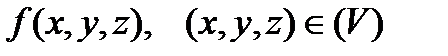 .
.
Разобьем 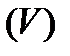 поверхностями на конечное количество частей
поверхностями на конечное количество частей 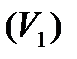 ,
, 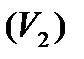 ,...,
,..., 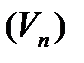 с объемами
с объемами 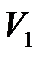 ,
, 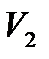 ,...,
,..., 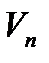 . В каждой части произвольно выберем промежуточные точки
. В каждой части произвольно выберем промежуточные точки 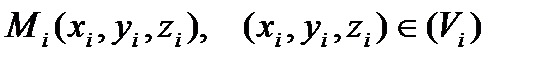 , и вычислим в них значения функции
, и вычислим в них значения функции 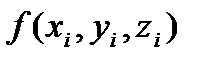 . Тогда
. Тогда
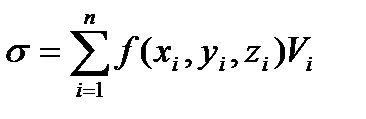
 называется интегральной суммой для тройного интеграла.
называется интегральной суммой для тройного интеграла.
Обозначим:
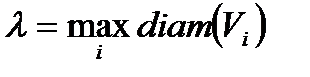 .
.
Определение. Если существует
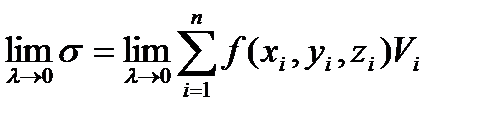 ,
,
который не зависит ни от того, как тело 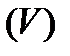 разбивалось на части, ни от выбора промежуточных точек
разбивалось на части, ни от выбора промежуточных точек 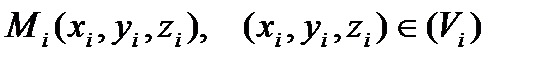 , то этот предел называется тройным интегралом от функции
, то этот предел называется тройным интегралом от функции 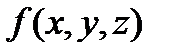 по области
по области 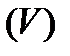 и обозначается:
и обозначается:
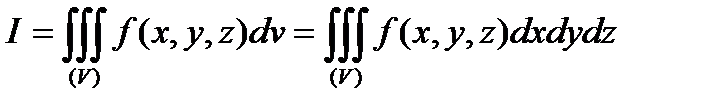 .
.
12
Дата добавления: 2015-08-21; просмотров: 494;
