Вычисление многомерных интегралов

Многие физические задачи содержат усреднение по многим переменным. Например, предположим, что нам известна зависимость от координаты и скорости полной энергии системы десяти взаимодействующих частиц. Поскольку в трехмерном пространстве каждая частица имеет по три компонента координаты и три компонента скорости, то полная энергия данной системы является функцией шестидесяти переменных. Следовательно, для вычисления средней энергии требуется вычислить шестидесятимерный интеграл. Если разделить область изменения каждой переменной на n отрезков, то в данном случае придется вычислять сумму по n⁶⁰ точкам. Совершенно очевидно, что для больших размерностей интегралов применять классические численные методы нельзя, тем не менее они используются, когда кратность интегралов не превышает пяти.

Простейший метод оценки многомерных интегралов заключается в сведении этих интегралов к произведению одномерных интегралов.

Рассмотрим двумерный интеграл вида

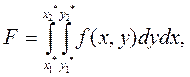(5.25)

где пределы y₁^* и y₂^*, вообще говоря, являются функциями от x: y₁^*= y₁^*(x), y₂^*= y₂^*(x).

Определим функцию g(x) как внутренний интеграл по y:

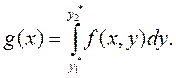(5.26)

Запишем исходный интеграл в виде:

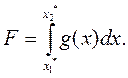(5.27)

Тогда алгоритм вычисления двухмерного интеграла выглядит следующим образом:

1) разбиваем интервал (x₁^*,x₂^*) на n малых отрезков Dx, а интервал (y₁^*,y₂^*) на m отрезков Dy;

2) для текущего x_i= x_i-1+Dx вычисляем y₁^*(x_i) и y₂^*(x_i);

3) вычисляем g(x_i):

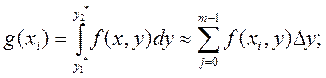(5.28)

4) вычисляем F_n:

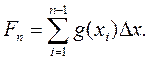(5.29)

Пояснение. Для вычисления одномерных интегралов в этой схеме использован метод прямоугольников.

Как уже отмечалось, классические методы непригодны при вычислении интегралов большой кратности. Большей эффективностью будет обладать при решении таких задач метод Монте-Карло. Предлагаем вам самостоятельно разработать алгоритм вычисления двухмерного интеграла этим методом (например, с использованием вычисления выборочного среднего).

Задание

Вычислите интеграл из предыдущего задания методом Монте-Карло.