Численное вычисление одномерных интегралов

Рассмотрим определенный интеграл вида

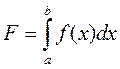. (5.13)

Для большинства подынтегральных функций f(x) вычислить аналитически данный интеграл не удается, и поэтому интеграл (5.13) нужно вычислять численно.

Классический метод численного интегрирования основан на геометрической интерпретации интеграла (5.13) как площади под графиком функции f(x) в пределах от x=a до x=b (рис. 5.3).

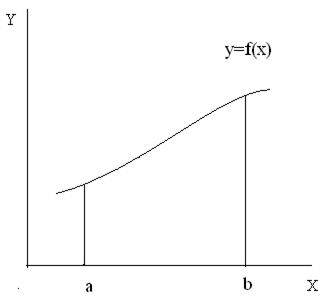
Рис. 5.3

Делим отрезок (a,b) на n равных отрезков Dx:

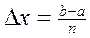. (5.14)

Тогда x₀=a, x_i=x_i+iDx, x_к=x_n (5.15)

Простейшей оценкой площади под кривой f(x) служит сумма площадей прямоугольников (рис.5.4).

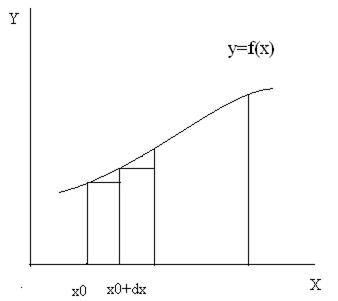
Рис. 5.4

В методе прямоугольников значение функции f(x) вычисляется в начале каждого отрезка (в точке слева), и оценка интеграла дается выражением

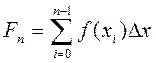. (5.16)

Модификацией метода прямоугольников является вычисление f(x) в средней точке каждого отрезка:

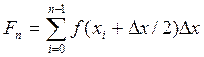. (5.17)

Другим приближением является формула трапеций, в которой интеграл оценивается вычислением площади трапеции со сторонами, равными значениям f(x) в начале и конце отрезка (рис.5.5).

S трапеции = (f(x₀)+ f(x₀+dx))/2.

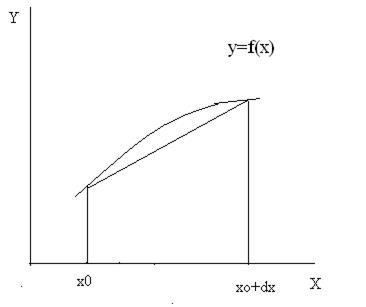
Рис. 5.5

Оценка интеграла дается выражением

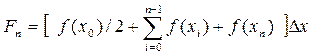. (5.18)

Очевидно, что точность вычисления интегралов вышеописанными методами определяется шагом сетки Dx: чем меньше его величина, тем с большей точностью мы вычисляем интеграл.

Задание

Вычислите любым из описанных выше методов интеграл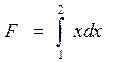

и сравните приближенный ответ с точным значением интеграла.