Пример моделирования физической системы

Рассмотрим моделирование процессов переноса тепла на примере остывания нагретого тела. Природа переноса тепла от тела к окружающему пространству включает в себя механизмы конвекции, излучения, испарения и теплопроводности. В том случае, когда разность температур между объектом и окружающей средой не очень велика, скорость изменения температуры объекта можно считать пропорциональной этой разности температур. Это утверждение можно сформулировать на языке дифференциального уравнения

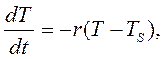(5.30)

где T – температура тела; T_S- температура окружающей среды; r – коэффициент пропорциональности, зависящий от механизма теплопередачи, площади тела и тепловых свойств самого тела. Знак минус в правой части уравнения означает, что температура нагретого тела может только убывать, если T >T_S .

Данное уравнение представляет собой дифференциальное уравнение первого порядка. Типичным методом решения таких уравнений является метод Эйлера. Запишем уравнения дискретной модели:

t_i=t_i-1+Dt,

T_ш=T_i-1-r(T_i-1-T_S)Dt, i=1, 2...m. (5.31)

Составим алгоритм решения задачи. Зафиксируем алгоритм на языке блок-схем (рис.5.8).

Рис. 5.8.

Пояснения к блок-схеме

На блок-схеме буквой t обозначается переменная, относящаяся к времени, t0, tk – начальный и конечный моменты времени расчетов; dt1, dt2 – период расчетов (т.е. интервал времени, через который выдается текущее значение переменных) и параметр дискретизации соответственно; N – количество точек расчетов; M – количество итераций метода Эйлера; переменные Temp, Temp_0, Temp_S – это текущая температура, начальная температура и температура окружающей среды соответственно.

Задание

1. Разработайте по данному алгоритму программу на каком-либо алгоритмическом языке.

2. Проведите экспериментальное измерение температуры нагретого тела (например, жидкости, помещенной в сосуд) в разные моменты времени.

3. Задавая различные значения коэффициента r в программе, подберите такое его значение, при котором ошибка расчета не превышает 10%.

4. Сделайте расчет в промежуточных точках (т.е. в точках, в которых не измерялась температура) и сравните с экспериментальными значениями.

5. Варьируя параметр дискретизации (шаг сетки) Dt, исследуйте, как влияет его значение на точность расчетов.

Задания

1. Постройте математическую модель движения планеты вокруг звезды, разработайте программу и исследуйте в компьютерном эксперименте выполнение законов Кеплера.

2. Постройте математическую модель колебаний одномерного гармонического осциллятора (груз на пружине, движущийся в горизонтальной плоскости), разработайте программу и исследуйте в компьютерном эксперименте и исследуйте влияние силы трения и периодической гармонической вынуждающей силы на колебания системы.

3. Постройте модель движения пробного заряда в электростатическом поле, созданным двумя другими зарядами, разработайте программу и исследуйте в компьютерном эксперименте поведение системы.

Заключение

Развитие техники базируется на достижениях физики. Поэтому четкое понимание логики постановки и решения физических вопросов необходимо для плодотворной деятельности современного инженера. Современная физика – обширная и разветвленная наука, но ее разделы имеют много общих черт. Знание характерных черт физики как науки облегчает ее освоение и помогает эффективно использовать ее методы и концепции.

1. Прежде всего, физика – наука опытная.

2. Все измерения в физике проводятся с ограниченной точностью. Ограничение точности ставит предел степени подробности информации, получаемой из опыта. Поэтому при каждом измерении указывается не только его результат, но и точность, с которой он получен.

3. На основании результатов физических экспериментов формулируются физические теории в виде физических законов. При этом каждый физический закон имеет определенную область применимости. Физические законы, имеющие наиболее обширные области применения, называют фундаментальными. Законы, действие которых ограничено узким кругом явлений, называются частными.

4. Для количественного описания физических явлений используются различные физические величины. Физические величины, подобно физическим законам, различаются по степени фундаментальности.

5. Для выражения количественных закономерностей в физике широко применяется математический аппарат. Лишь малое число уравнений имеют аналитическое решение, и в этом случае приходится искать приближенное решение, опираясь на методы численного анализа и компьютерные расчеты.

6. Типичной задачей любого раздела физики является ответ на вопрос, как будет вести себя исследуемая физическая система в данных условиях. Для того чтобы сформулировать и решить такую задачу, необходимо задать для исследуемой системы ее состояние и уравнения движения. Состояние системы определяется набором независимых друг от друга физических величин, описывающих эту систему. Уравнения движения описывают изменение состояния системы во времени. Решить уравнения движения – значит, найти временную зависимость независимых параметров, входящих в уравнения.

Компьютер не только позволил нам полностью осознать единство физики, но и единство всех природных процессов, так как в их основе лежат фундаментальные закономерности, описываемые одинаковыми математическими законами.

СПИСОК ЛИТЕРАТУРЫ

1. Винер Н. Кибернетика, или Управление и связь в животном и машине / Винер Н. – М.., 1968.

2. Острейковский В.А. Информатика / Острейковский В.А. М.., 2000.

3. Кибернетика. Становление информатики. Серия “Кибернетика – неограниченные возможности и возможные ограничения” / М.., 1986.

4. Джордж Ф. Основы кибернетики / Джордж Ф. – М.., 1984.

5. Блюменау Д.И. Информация и информационный сервис / Блюменау Д.И. –М.., 1989.

6. Трасковский А.В. Устройство, модеринизация, ремонт IBM PC/СПб, 2003.

7. Кенин А.М. IBM PC для пользователей / Кенин А.М., Печенкина Н.С. – Екатеринбург, 1997.

8. Кенин А.М. Windows 95/NT для польз

ователей или как научиться работать на компьютере / Кенин А.М. – Екатеринбург. 1998.

9. Дайитбегов Д.М. Основы алгоритмизации и алгоритмические языки / Дайитбегов Д.М., Черноусов Е.А. – М.., 1992.

10. Хакен Г. Информация и самоорганизация / Хакен Г. – М.., 1991.

11. Лебедев А.Н. Моделирование в научно-технических исследованиях / Лебедев А.Н. – М.., 1989.

12. Гулд Х., Тобочник Я. Компьютерное моделирование в физике / Гулд Х., Тобочник Я. Часть 1-2. – М.., 1990.

13. Самарский А.А. Введение в численные методы / Самарский А.А. – М.., 1989.

14. Кибардин А.В. Работа пользователя в среде Windows.: Методические указания для самостоятельной работы студентов по курсу “Информатика” / Кибардин А.В. – Екатеринбург, 1998.15. Кибардин А.В. Компьютерный эксперимент в физике. Методические указания для самостоятельной работы студентов по курсу “Информатика” / Кибардин А.В. – Екатеринбург, 2002.

СОДЕРЖАНИЕ

Предисловие.. 3

ЧАСТЬ 1. ВВЕДЕНИЕ.. 4

1.1 Определение информатики. Понятие информации и информационной технологии. Формула Шеннона. Предмет и задачи информатики. 4

1.2 Техническая база информатики. 9

Из истории создания и развития ЭВМ.. 9

Классификация ЭВМ.. 10

Классическая архитектура ЭВМ общего назначения. 11

Структура шин. 14

Структура ЭВМ 5-го поколения. 17

Системы обработки данных. 18

1.3 Программное обеспечение информатики. 26

Операционные системы (ОС) 27

Инструментальные языки и системы программирования. 28

Системы программирования. 29

ЧАСТЬ 2. Математические основы информатики... 30

2.1 Теория формальных структур данных и алгоритмов их обработки. 30

Основные понятия теории алгоритмов. 30

Общая характеристика изобразительных средств алгоритмов. 32

Основные типы вычислительных процессов. 36

2.2 Системы счисления. 40

Позиционные системы счисления. 41

Смешанные системы счисления. 43

Перевод чисел из одной системы счисления в другую.. 44

Форматы представления и преобразования информации. 46

2.3 Способы разработки алгоритмов. 48

чАСТЬ 3. пЕРСОНАЛЬНЫЕ эвм... 50

3.1 Из истории создания персональных компьютеров. 50

3.2 Структура ПЭВМ.. 51

3.3 Внешние устройства ПЭВМ.. 54

ЧАСТЬ 4. Работа пользователя в операционной системе Windows: начальные сведения.. 59

4.1 Введение. 59

4.2 Загрузка Windows. 59

Рабочий стол. 60

Изображения курсора мыши. 61

Приемы работы с мышью.. 61

Элементы рабочего стола. 62

Пиктограммы.. 62

Панель задач. 63

Основное меню панели задач. 64

Окна задач. 66

Основные команды меню.. 68

Вызов и завершение работы программ. 69

4.3 Операции с папками и файлами. 70

Проводник. 70

Пиктограммы, отображающие структуру диска. 71

Операции с папками. 72

Копирование, перемещение файлов и папок. 72

Удаление файлов и папок и их восстановление. 74

4.4 Стандартные программы Windows. 75

Калькулятор. 75

Блокнот. 75

Текстовый редактор Word Pad. 75

Графический редактор Paint 76

4.5 Завершение работы в Windows. 76

Часть 5. Компьютерное моделирование в физических исследованиях... 78

5.1 Роль эксперимента в физических исследованиях. Виды экспериментальных исследований. 78

5.2 Основы теории моделирования. 80

Базовые понятия. 80

Классификация моделей. 81

5.3 Математическое моделирование и компьютерный эксперимент. 84

Понятие математической модели. 84

Особенности математических моделей. 87

5.4 Вычислительный алгоритм. Введение в численные методы.. 89

Базовые понятия численных методов. 91

Численное решение линейных дифференциальных уравнений. 92

Численное вычисление одномерных интегралов. 94

Метод Монте-Карло. 97

Вычисление многомерных интегралов. 100

5.5 Технология программирования вычислительных задач. 101

5.6 Точность компьютерного эксперимента. 104

Погрешности компьютерного эксперимента. 104

Требования к вычислительным алгоритмам. 106

5.7 Пример моделирования физической системы.. 107

5.8 Заключение. 110

СПИСОК ЛИТЕРАТУРЫ... 112

СОДЕРЖАНИЕ.. 114

Учебное издание

Гольдштейн Сергей Людвигович

Кибардин Алексей Владимирович