Определение интегралов, зависящих от параметра
Пусть функция 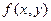 определена в прямоугольнике
определена в прямоугольнике 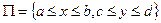 . Пусть при каждом фиксированном
. Пусть при каждом фиксированном 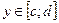 существует
существует  . Очевидно, что для каждого значения
. Очевидно, что для каждого значения 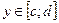 будет существовать свое значение интеграла. Таким образом мы получаем функцию переменной (параметра)
будет существовать свое значение интеграла. Таким образом мы получаем функцию переменной (параметра) 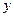 , определенную на отрезке
, определенную на отрезке 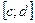 . Обозначим:
. Обозначим:
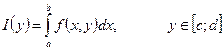 (1)
(1)
Поставим следующую задачу: исходя из свойств функции 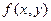 , получить сведения о функции
, получить сведения о функции 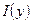 .
.
Предположим также, что при каждом фиксированном 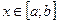 существует
существует 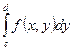 . Данный интеграл будет представлять собой функцию переменной (параметра)
. Данный интеграл будет представлять собой функцию переменной (параметра) 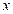 . Введем обозначение
. Введем обозначение
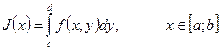 (2)
(2)
§2. Предельный переход под знаком интеграла
Теорема. Пусть функция 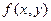 непрерывна в прямоугольнике
непрерывна в прямоугольнике  и
и 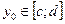 . Тогда
. Тогда
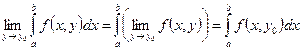 (1)
(1)
Доказательство. Существование интеграла для каждого значения 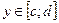 следует из непрерывности подынтегральной функции.
следует из непрерывности подынтегральной функции.
Выберем произвольное 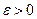 и зафиксируем
и зафиксируем 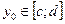 . Функция
. Функция 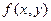 непрерывна на замкнутом прямоугольнике, следовательно, по теореме Кантора она является равномерно непрерывной. Тогда существует такое число
непрерывна на замкнутом прямоугольнике, следовательно, по теореме Кантора она является равномерно непрерывной. Тогда существует такое число 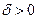 , зависящее только от
, зависящее только от 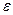 , такое, что для любых двух точек
, такое, что для любых двух точек 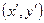 и
и 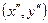 из прямоугольника
из прямоугольника  , для которых
, для которых 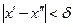 и
и 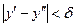 будет выполняться неравенство:
будет выполняться неравенство:
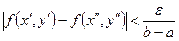 . (2)
. (2)
Положим 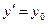 ,
, 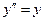 , где для произвольного
, где для произвольного 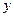 выполняется неравенство
выполняется неравенство 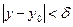 . Значения первой переменной выберем равными, т.е.
. Значения первой переменной выберем равными, т.е. 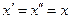 , где
, где 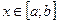 . Заметим что,
. Заметим что, 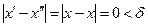 . Тогда неравенство (2) примет вид
. Тогда неравенство (2) примет вид
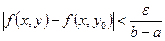 (3)
(3)
для любого 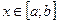 , если
, если 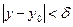 и
и 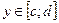 . Оценим разность интегралов
. Оценим разность интегралов
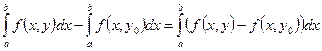 .
.
С учетом неравенства (3), получаем
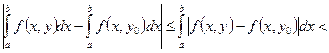
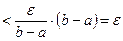 .
.
В ходе доказательства мы получили, что для 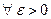 существует
существует 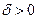 , такое что из неравенства
, такое что из неравенства 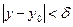 ,
, 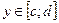 следует неравенство
следует неравенство
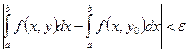 .
.
Следовательно
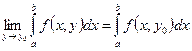
Теорема доказана.
Замечание.
Аналогичным образом доказывается симметричное (относительно переменных) утверждение: если функция 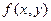 непрерывна в прямоугольнике
непрерывна в прямоугольнике  и
и 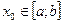 , то
, то
Дата добавления: 2015-08-11; просмотров: 654;
