D-разбиение по двум параметрам
В ряде случаев необходимо выяснить влияние на устойчивость системы не одного параметра, а двух. Предположим, что эти параметры линейно входят в характеристическое уравнение и ему можно придать вид
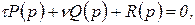 (2.3.5)
(2.3.5)
где 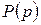 ,
, 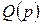 ,
, 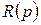 — полиномы от p; τ и ν — варьируемые параметры.
— полиномы от p; τ и ν — варьируемые параметры.
Граница D-разбиения в плоскости τ и ν согласно (2.3.1) определяется уравнением
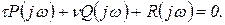 (2.3.6)
(2.3.6)
Обозначим
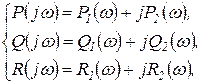 (2.3.7)
(2.3.7)
тогда уравнение (2.3.6) можно разбить на два уравнения, приравняв раздельно вещественную и мнимую части нулю:
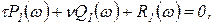 (2.3.8)
(2.3.8)
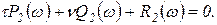 (2.3.9)
(2.3.9)
Решая систему уравнений (2.3.8) и (2.3.9) относительно τ и ν, получим
 (2.3.10)
(2.3.10)
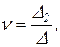 (2.3.11)
(2.3.11)
где
 (2.3.12)
(2.3.12)
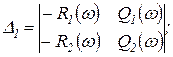 (2.3.13)
(2.3.13)
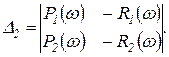 (2.3.14)
(2.3.14)
При 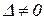 для каждого значения ω по уравнениям (2.3.10)–(2.3.14) можно определить величины τ и ν и, таким образом, в плоскости τ и ν построить границу D-разбиения.
для каждого значения ω по уравнениям (2.3.10)–(2.3.14) можно определить величины τ и ν и, таким образом, в плоскости τ и ν построить границу D-разбиения.
Из (2.3.10)–(2.3.14) видно, что 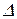 ,
, 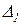 и
и 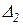 являются нечётными функциями ω, ибо вещественные части
являются нечётными функциями ω, ибо вещественные части 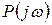 ,
, 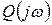 и
и 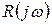 — чётные функции ω, а мнимые — нечётные функции. Отсюда следует согласно (2.3.10) и (2.3.11), что τ и ν являются чётными функциями ω.
— чётные функции ω, а мнимые — нечётные функции. Отсюда следует согласно (2.3.10) и (2.3.11), что τ и ν являются чётными функциями ω.
Рассмотрим случай, когда при некотором значении ω определитель 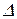 равен нулю (
равен нулю ( 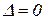 ). Тогда, если при этом значении ω определители
). Тогда, если при этом значении ω определители 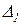 и
и 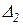 не равны нулю, то точка границы D-разбиения в плоскости τ и ν уходит в бесконечность. Если же при этом значении ω определители
не равны нулю, то точка границы D-разбиения в плоскости τ и ν уходит в бесконечность. Если же при этом значении ω определители 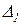 и
и 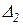 также будут равны нулю, то τ и ν согласно (2.3.10) и (2.3.11) будут неопределёнными. Это соответствует тому, что уравнения (2.3.8) и (2.3.9) становятся эквивалентными и определяют собой прямую в плоскости τ и ν, т.е. для рассматриваемого значения ω (при котором
также будут равны нулю, то τ и ν согласно (2.3.10) и (2.3.11) будут неопределёнными. Это соответствует тому, что уравнения (2.3.8) и (2.3.9) становятся эквивалентными и определяют собой прямую в плоскости τ и ν, т.е. для рассматриваемого значения ω (при котором 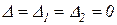 ) получим в плоскости τ и ν не точку, а прямую, называемую особой прямой.
) получим в плоскости τ и ν не точку, а прямую, называемую особой прямой.
В большинстве практических задач особые прямые отвечают значению 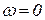 и
и 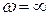 . В этом случае коэффициенты, соответствующие свободному и старшему членам характеристического уравнения, зависят от τ и ν, и для получения уравнений этих особых прямых необходимо указанные коэффициенты приравнять нулю. Первый коэффициент (свободный член) дает прямую для
. В этом случае коэффициенты, соответствующие свободному и старшему членам характеристического уравнения, зависят от τ и ν, и для получения уравнений этих особых прямых необходимо указанные коэффициенты приравнять нулю. Первый коэффициент (свободный член) дает прямую для 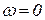 , второй — для
, второй — для 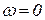 .
.
Рассмотренное выше решение системы уравнений (2.3.8) и (2.3.9) может быть проведено графически. На рисунке 2.3.3 показаны прямые 1 и 2 для заданного значения ω, соответствующие уравнениям (2.3.8) и (2.3.9) для трёх случаев:
1) 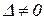 и
и 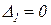 ,
,
2) 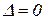 и
и 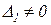 ,
,
3) 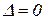 и
и 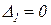 .
.
В первом случае точка пересечения прямых 1 и 2 определяет значения τ и ν для заданного значения ω; во втором случае прямые 1 и 2 параллельны и определяют значения τ и ν, равные бесконечности; в третьем случае прямые 1 и 2 сливаются друг с другом, и, таким образом, для заданного значения ω получается прямая, а не одна точка.
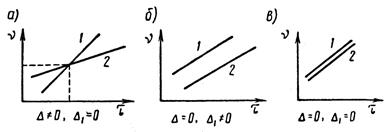
Рисунок 2.3.3 – Особые прямые
Правила штриховки границы D-разбиения. Граница D-разбиения штрихуется слева при обходе в сторону возрастающих ω, если главный определитель 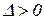 , и справа, если
, и справа, если 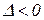 . Так как граница D-разбиения для положительных и отрицательных значений ω совпадает (величины τ и ν — чётные функции ω, а
. Так как граница D-разбиения для положительных и отрицательных значений ω совпадает (величины τ и ν — чётные функции ω, а 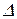 — нечётная функция), то она штрихуется дважды с одной и той же стороны (рисунок 2.3.4).
— нечётная функция), то она штрихуется дважды с одной и той же стороны (рисунок 2.3.4).
При 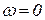 всегда
всегда 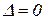 , и через точку, соответствующую
, и через точку, соответствующую 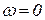 (и
(и 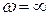 ), чаще всего, как указывалось, проходят особые прямые. Штриховка этих особых прямых ординарная и производится так, чтобы вблизи точки сопряжения прямой и кривой заштрихованные и незаштрихованные стороны прямой и кривой были направлены друг к другу (рисунок 2.3.4, а, б, в).
), чаще всего, как указывалось, проходят особые прямые. Штриховка этих особых прямых ординарная и производится так, чтобы вблизи точки сопряжения прямой и кривой заштрихованные и незаштрихованные стороны прямой и кривой были направлены друг к другу (рисунок 2.3.4, а, б, в).
В тех случаях, когда при 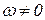
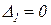 , а
, а 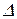 проходит через нуль и меняет знак (это сравнительно редкий случай), появляется особая прямая; она штрихуется в этом случае по сформулированному выше правилу, но двойной штриховкой (рисунок 2.3.4, г).
проходит через нуль и меняет знак (это сравнительно редкий случай), появляется особая прямая; она штрихуется в этом случае по сформулированному выше правилу, но двойной штриховкой (рисунок 2.3.4, г).
Если же при 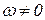
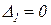 , а
, а 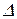 проходя через нуль, не меняет знака, то особая прямая не штрихуется и выбрасывается из рассмотрения (рисунок 2.3.4, д).
проходя через нуль, не меняет знака, то особая прямая не штрихуется и выбрасывается из рассмотрения (рисунок 2.3.4, д).
При построении границы D-разбиения по двум параметрам следует правильно ориентировать оси. Для проведенной выше записи уравнений τ следует откладывать по оси абсцисс, ν — по оси ординат. В случае перемены местами осей τ и ν соответственно изменяется ориентация штриховки относительно правой и левой сторон.
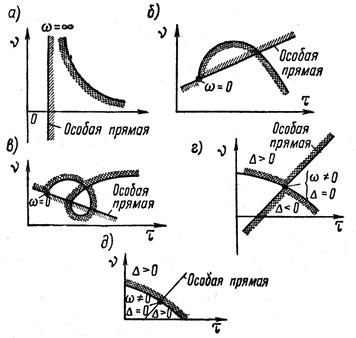
Рисунок 2.3.4 – Штриховка границы D-разбиения
Дата добавления: 2015-08-21; просмотров: 4087;
