Косвенные методы исследования качества процессов управления. Интегральные оценки качества переходных процессов
Рассмотрим переходную составляющую процесса управления, определение которой иллюстрируется рисунке 2.6.1,
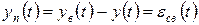 (2.6.1)
(2.6.1)
за весь теоретический интервал ее существования  . Естественно, что вычисление интегральных оценок должно быть обеспечено заданием структуры и параметров системы (дифференциальное уравнение, структурная схема или передаточная функция), воздействия на входе (функция времени или ее изображение по Лапласу) и начальных условий. Решение дифференциального уравнения при этом не требуется.
. Естественно, что вычисление интегральных оценок должно быть обеспечено заданием структуры и параметров системы (дифференциальное уравнение, структурная схема или передаточная функция), воздействия на входе (функция времени или ее изображение по Лапласу) и начальных условий. Решение дифференциального уравнения при этом не требуется.
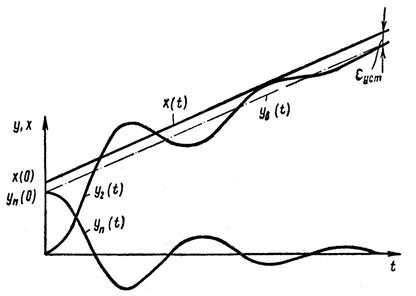
Рисунок 2.6.1 – Кривая переходного процесса
Линейные интегральные оценки. Линейной интегральной оценкой переходной составляющей 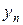 называется определенный интеграл вида
называется определенный интеграл вида
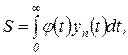 (2.6.2)
(2.6.2)
где 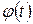 заранее заданная функция времени — функция веса.
заранее заданная функция времени — функция веса.
Практическое распространение получили линейные интегральные оценки
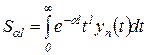
преимущественно вида
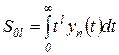 (2.6.3)
(2.6.3)
с функцией веса 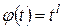 .
.
Простейшая из этих оценок
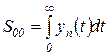 (2.6.4)
(2.6.4)
равна площади переходного процесса, заштрихованной на рисунке 2.6.2 с учетом знака 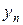 . Для монотонных процессов (рисунок 2.6.2, а) эта оценка может служить характеристикой качества системы.
. Для монотонных процессов (рисунок 2.6.2, а) эта оценка может служить характеристикой качества системы.
Оценка
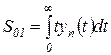 (2.6.5)
(2.6.5)
равна моменту площади 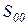 относительно начала координат. Отношение
относительно начала координат. Отношение
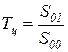
определяет положение центра тяжести фигуры, заштрихованной на рисунке 2.6.2, и может служить характеристикой быстродействия системы при монотонных процессах управления (см. рисунок 2.6.2, а).
Старшие оценки (2.6.3) определяют моменты l-го порядка функции 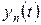 , где
, где 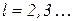
Линейные интегральные оценки можно вычислить по формуле
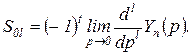 (2.6.6)
(2.6.6)
Согласно (2.6.6), оценка
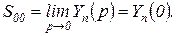 (2.6.7)
(2.6.7)
Применение линейных интегральных оценок практически ограничено, поскольку они приемлемы только для монотонных процессов. Из рисунка 2.6.2, б ясно, что для колебательного процесса значение 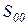 и других линейных оценок может быть малым при плохом затухании и больших перерегулированиях. Установить заранее монотонность процессов в исследуемой системе довольно трудно, что еще более ограничивает непосредственное применение этих оценок. От этого недостатка свободны квадратичные интегральные оценки.
и других линейных оценок может быть малым при плохом затухании и больших перерегулированиях. Установить заранее монотонность процессов в исследуемой системе довольно трудно, что еще более ограничивает непосредственное применение этих оценок. От этого недостатка свободны квадратичные интегральные оценки.
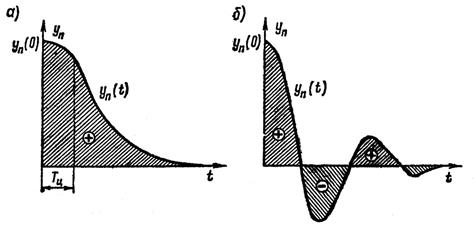
Рисунок 2.6.2 – Линейные интегральные оценки
Квадратичные интегральные оценки. Квадратичные интегральные оценки имеют вид

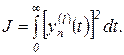 (2.6.8)
(2.6.8)
Простейшая квадратичная интегральная оценка
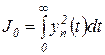 (2.6.9)
(2.6.9)
характеризует протекание переходного процесса так, как это представлено на рисунке 2.6.3. Её численное значение, равное площади, заштрихованной на этом рисунке, учитывает абсолютное значение отклонения 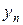 , что позволяет применять оценку
, что позволяет применять оценку 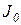 также и к колебательным системам.
также и к колебательным системам.
Интеграл проще всего определяется с помощью теоремы Релея, из которой
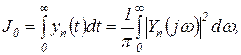 (2.6.10)
(2.6.10)
где  — амплитудный спектр переходной составляющей на выходе системы управления.
— амплитудный спектр переходной составляющей на выходе системы управления.
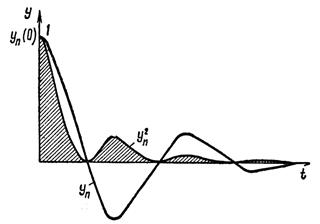
Рисунок 2.6.3 – Квадратичная интегральная оценка
В большинстве случаев изображение 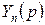 — дробно-рациональная функция
— дробно-рациональная функция
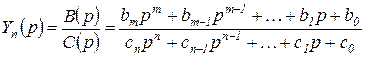 (2.6.11)
(2.6.11)
и формула (2.6.10) принимает вид
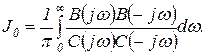 (2.6.12)
(2.6.12)
Интегралы вида (2.6.12) в функции коэффициентов 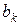 и
и 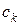 , вычисленные для
, вычисленные для 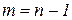 и
и  , представлены в Приложении 2.
, представлены в Приложении 2.
Наименьшее, нулевое значение оценки 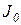 согласно (2.6.9) достигается при
согласно (2.6.9) достигается при 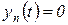 во всех точках, кроме
во всех точках, кроме 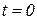 . Такой процесс не может быть принят в качестве эталона сравнения, поскольку чрезмерное быстродействие в линейной системе приводит к недопустимым и практически нереализуемым перенапряжениям и перегрузкам.
. Такой процесс не может быть принят в качестве эталона сравнения, поскольку чрезмерное быстродействие в линейной системе приводит к недопустимым и практически нереализуемым перенапряжениям и перегрузкам.
От перечисленных выше недостатков свободна квадратичная интегральная оценка
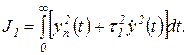 (2.6.13)
(2.6.13)
Увеличение точности расчётов обеспечивается применением одной из старших квадратичных интегральных оценок
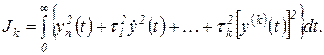
Оценка 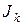 может быть вычислена как сумма
может быть вычислена как сумма
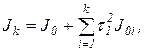 (2.6.14)
(2.6.14)
компоненты которой
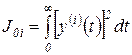
определяются по изображению 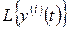 точно так же, как оценка
точно так же, как оценка 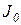 .
.
Дата добавления: 2015-08-21; просмотров: 1130;
