Разбиение по одному (комплексному) параметру

В некоторых случаях необходимо выяснить влияние какого-либо параметра 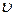на устойчивость системы. Предположим так же, как и при построении корневого годографа, что этот параметр входит линейно в характеристическое уравнение, которому можно придать вид

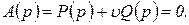(2.3.2)

Границы D-разбиения согласно (2.3.1) определяются урав­нением

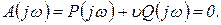(2.3.3)

Отсюда

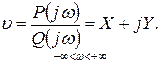(2.3.4)

При построении границы D-разбиения достаточно построить ее для положительных значений ω ( 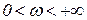) и затем до­полнить зеркальным отображением построенного участка отно­сительно действительной оси. Практически обычно интересует D-разбиение не всей комплекс­ной плоскости 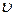, а лишь её действительной оси, которой отве­чают действительные значе­ния .

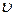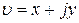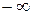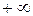На рисунке 2.3.2 показан вид границы D-разбиения в плос­кости . При измене­нии ω от до в плос­кости р мнимая ось проходит снизу вверх, при этом левая полуплоскось остается слева. Будем штриховать мнимую ось слева (рисунок 2.3.2, б). Такому движению по мнимой оси соот­ветствует движение по границе D-разбиения в плоскости 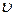(рисунок 2.3.2, а), которую будем также штриховать слева по обходу при изменении ω от 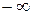до .

Если в плоскости пересекать границу D-разбиения по на­правлению штриховки (стрелка 1, рисунок 2.3.2, а), то в плоскости корней один корень переходит из правой полуплоскости в левую. Если же в плоскости пересекать границу D-разбиения против штриховки (стрелка 2, рисунок 2.3.2, а), то в плоскости корней один корень переходит из левой полуплоскости в правую.

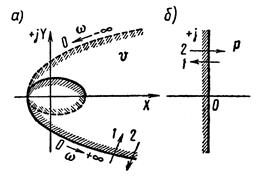
Рисунок 2.3.2 – Граница D-разбиения по одному параметру

Направление штриховки и число штриховок определяют на­правление перехода корней через мнимую ось и их число. По­этому для разметки областей 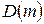достаточно знать распреде­ление корней относительно мнимой оси при каком-либо произ­вольном значении параметра. Переходя в плоскости 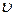от этого значения параметра 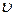к любому другому, по числу пересечений границы D-разбиения и направлению штриховки, можно определить значение m в любой точке. Областью устойчивости будет область 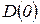и претендентом на эту область (отрезок) — область (отрезок), к которой направлена штри­ховка.

Обычно в линейных задачах изменяемый параметр является вещественным (коэффициент усиления, постоянная времени) и практический интерес имеет область D-разбиения, прилегаю­щая к оси X. Рассмотрение всей области комплексного пара­метра представляет интерес для нелинейных задач, где может быть использован полученный результат.