Влияние параметров системы на её устойчивость. Метод D-разбиения

Все приведённые критерии устойчивости дают воз­можность при заданных параметрах системы делать заключение о том, устойчива она или нет. С помощью этих критериев воз­можно проследить влияние некоторых параметров на устойчи­вость системы, определить предельные значения коэффициента усиления системы и времени запаздывания.

Для исследования влияния различных параметров системы на ее устойчивость разработаны специальные методы, позволяю­щие облегчить исследование.

Рассмотрение влияния параметров на устойчивость системы может производиться путём анализа числа корней характери­стического уравнения, лежащих в правой полуплоскости, в про­странстве параметров системы.

Этот метод получил название метода D-разбиения пространства параметров.

Пусть дано характеристическое уравнение n-й степени

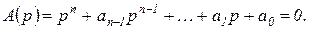
При заданном значении коэффициентов уравнения в общем случае оно имеет m корней в правой полуплоскости, и, сле­довательно, 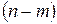корней в левой полуплоскости. При из­менении коэффициентов уравнения корни его перемещаются в плоскости корней, описывая корневые годографы. При не­котором значении коэффициентов один из корней попадает в начало координат или пара корней попадет на мнимую ось и поэтому значение этих коэффициентов удовлетворяет урав­нению

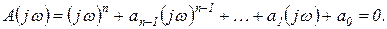(2.3.1)

Уравнению (2.3.1) в 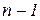-мерном пространстве коэффи­циентов, по осям которого отложены a₀, a₂, ..., a_n-1, соот­ветствует точка при данном значении ω и гиперповерхность — при изменении ω в пределах от 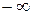до .

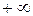Если перемещаться в пространстве коэффициентов, т.е. если менять коэффициенты уравнения, то при некотором их значении мы пересечем гиперповерхность 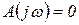и, следо­вательно, пара (или один корень) будет переходить из пра­вой (левой) полуплоскости корней в левую (правую) полу­плоскость корней.

Рассмотрим более подробно случай, когда 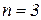и харак­теристическое уравнение имеет вид

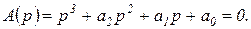
Каждому значению коэффициентов a₀, a₁ и a₂ в трёхмер­ном пространстве коэффициентов (рисунок 2.3.1) соответствует точка. Этому значению коэффициентов уравнения соответст­вует определенное расположение корней уравнения в плоскости корней (рисунок 2.3.1,б). Точке М соответствуют корни m₁, m₂ и m₃,точке N — корни n₁, n₂ и n₃. При некоторых значениях коэффициентов один или пара корней окажутся на мнимой оси, т.е. корни будут иметь вид 0 или 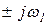и, следовательно, соответствующая точка в пространстве коэффи­циентов будет удовлетворять уравнению

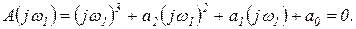
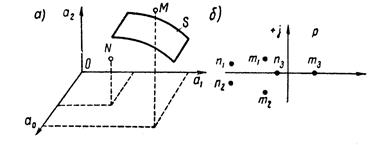
Рисунок 2.3.1 – Расположение корней характеристического уравнения

Этому уравнению при 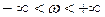соответствует поверх­ность S, часть которой показана на рисунке 2.3.1, а. При изменении коэффициентов корни характеристического уравнения тоже из­меняются и попадают на мнимую ось только тогда, когда точка в пространстве коэффициентов попадает на поверхность S. При пересечении точкой поверхности корни переходят из одной по­луплоскости корней в другую. Отсюда следует, что поверх­ность S разделяет пространство коэффициентов на области, каж­дой точке которых соответствует характеристическое уравнение 3-й степени, имеющее определенное число корней в правой и ле­вой части плоскости корней. Обозначим эти области через 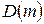, где m — число корней уравнения в правой полуплоскости. Для уравнения 3-й степени можно наметить в пространстве коэффи­циентов четыре области: 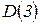, , 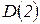, 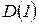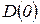. Последняя область является областью устойчивости. Такое разбиение про­странства на области с различным значением m называется D-разбиением.

Для уравнений более высокой степени 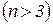вместо обыч­ного трехмерного пространства приходится рассматривать мно­гомерное пространство и гиперповерхности, разбивающие это пространство на области.

Это значительно усложняет задачу, и рассмотрение теряет наглядность. Если изменяются не все коэффициенты, а часть их, например, два a₁ и a₂, а 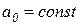, то вместо поверхности по­лучаем кривую, которая является сечением поверхности S плос­костью .

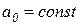Переход через границу D-разбиения соответствует, как ука­зывалось, переходу корней уравнения через мнимую ось. Поэто­му уравнение границы D-разбиения, в соответствии с ранее ска­занным, имеет вид уравнения (2.3.1) и, следовательно, может быть получено из характеристического уравнения 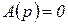за­меной р на jω. По полученным в параметрической форме урав­нениям можно построить границу D-разбиения, задаваясь значе­ниями ω от 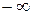до .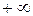

Аналогичным способом можно построить D-разбиение в про­странстве не коэффициентов уравнения, а параметров системы, от которых зависят коэффициенты характеристического уравне­ния, например, в координатах T₁, T₂, k и т.д.