Качество регулирования при стандартных воздействиях

Переходная функция и статическая ошибка. Общераспространенность оценки качества системы по её пере­ходной функции объясняется в основном простотой и нагляд­ностью эксперимента для получения этой характеристики, как на модели системы, так и в реальных условиях. Следует, однако, отметить, что в реальных условиях абсолютную величину воз­действия приходится выбирать достаточно малой, чтобы в про­цессе его отработки система не вышла за границы области, в которой линеаризованные уравнения с заданной точностью со­ответствуют математическому описанию физической (нелиней­ной) системы. При низком уровне полезного воздействия различ­ные помехи могут совершенно исказить результат эксперимента. В этих случаях прибегают к испытаниям модели системы, к кос­венному определению переходной функции по частотным харак­теристикам или же к специальной методике определения 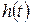по результатам статистической обработки многочисленных экс­периментов.

Многообразие переходных функций автоматических систем можно разбить на три типа: колебательные с перерегулирова­нием, колебательные без перерегулирования и монотонные.

Рассмотрим применение показателей качества к оценке пе­реходной функции системы.

Точность системы автоматического регулирования при отра­ботке ступенчатого сигнала 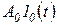оценивается статической ошибкой системы .

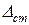Статическая ошибка по управляющему воздействию. Согласно (2.4.2), ошибка по управляющему воздействию

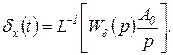
и по теореме о предельном значении статическая ошибка

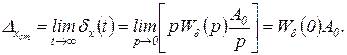(2.4.11)

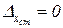при условии, что в (2.4.7)

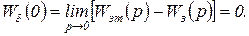(2.4.12)

Системы, обладающие этим свойством, называются астатическими по управляющему воздействию.

Если же 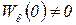, то систему называют статической, при этом в виду, что согласно (2.4.11) установившееся значение её выхода при отработке постоянного управляющего сигнала отличается от требуемого (эталонного) значения тем больше, чем больше уровень входного сигнала.

В системах автоматического регулирования, для которых справедливо условие (2.4.9),

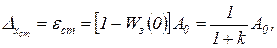(2.4.13)

где k — коэффициент усиления разомкнутой системы.

Статическая ошибка по возмущению. При исследова­нии точности по возмущению из (2.4.2) и (2.4.10) следует, что

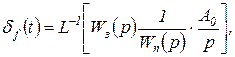(2.4.14)

где 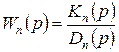― передаточная функция участка системы между управляющим входом и входом исследуемого воз­мущения.

Статическая ошибка

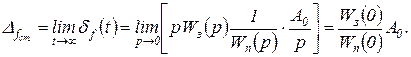(2.4.15)

Для системы, астатической по возмущению, требуется, чтобы

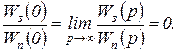(2.4.16)

Для того чтобы система реагировала на постоянный управ­ляющий сигнал, необходимо, чтобы 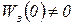, откуда усло­вие (2.4.16) эквивалентно требованию

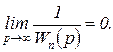(2.4.17)

Если условие (2.4.16) не выполняется, то систему назы­вают статической по возмущению и статическую ошибку вычисляют по формуле

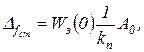(2.4.18)

где .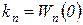

Как видно из структурной схемы, изображенной на рисунке 2.4.1, участок 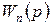представляет собой обратную связь по рассматри­ваемому возмущению (участок от выхода системы до ввода возмущения), поэтому из (2.4.18) следует, что точность стати­ческой системы тем выше, чем больше коэффициент усиления цепи обратной связи (коэффициент усиления пропорциональ­ного регулятора). Однако возможность увеличения коэффици­ента усиления в контуре статической системы для повышения её точности по управляющему входу и возмущениям ограни­чена условием качества переходных процессов и, в пределе, условием устойчивости

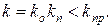(2.4.19)

Это приводит к необходимости коррекции систем автоматиче­ского управления, т.е. к такому изменению структуры и па­раметров, при котором можно получить одновременно и высо­кую точность, и требуемое качество протекания переходных процессов.

Импульсная переходная функция. Качество си­стем, подверженных импульсному (ударному) воздействию, а также систем, выход которых должен воспроизводить интеграл от входного сигнала, естественно оценивать по реакции системы на импульс. Системы управления с таким режимом работы ши­роко распространены в практике, кроме того, импульсное воздействие зачастую удобно при эксперименталь­ном определении качества реальных систем и их моделей.

Для определения качества по импульсной переходной функции могут быть применены те же оценки, что и для определения рассогласования системы.

Для устойчивых замкнутых систем статическое отклонение весовой функции

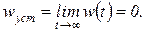(2.4.20)

Нарушение этого условия характеризует интегрирующую (нейтральную) систему, для которой

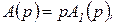(2.4.21)

и уравнение (1.26) может быть записано в форме

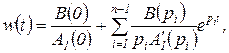(2.4.22)

откуда следует, что весовая функция нейтральной системы (интегратора) характеризует её качество так же, как переход­ная функция — качество устойчивой системы.

Кинетическая ошибка. Точность астатических си­стем определяют по установившейся погрешности при отра­ботке сигнала постоянной скорости, т.е. при воздействии

откуда

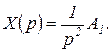(2.4.23)

Установившаяся погрешность при этих условиях называется кинетической ошибкой .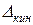

Кинетическая ошибка по управляющему воздействию 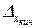служит основной характеристикой точности многих автомати­ческих систем, в частности следящего привода.

Из (2.4.2) и (2.4.23) следует, что

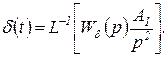(2.4.24)

По теореме о предельном значении кине­тическая ошибка

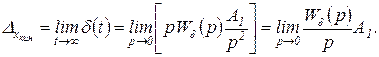(2.4.25)

Поскольку рассматривается астатическая система, то 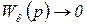при 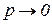по меньшей степени так же, как p. Раскрыв для этого случая неопределенность по правилу Лопиталя, получим

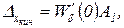(2.4.26)

где

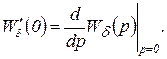
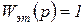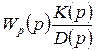Рассмотрим астатическую систему автоматического регулирования при и , где

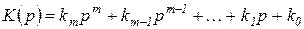
и

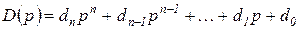
— полиномы от p, причем .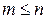

Передаточная функция

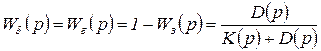
соответствует условию (2.4.12), если, по крайней мере 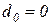, откуда ; .

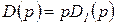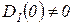Очевидно, что

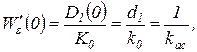
где 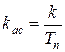с^–1 — коэффициент усиления разомкнутой астатической системы, или её добротность. Из (2.4.26) в этом случае следует, что

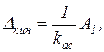(2.4.27)

т.е. что кинетическая ошибка астатической системы регули­рования пропорциональна скорости равномерной заводки и об­ратно пропорциональна добротности системы. При современных требованиях к точности следящего привода добротность до­стигает несколько тысяч. Очевидно, что реализация таких систем без корректирующих устройств невозможна.

Кинетическая ошибка по возмущению определяется анало­гично, с заменой 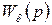на .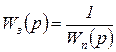

Динамическая ошибка. Погрешность системы в установившемся режиме отработки произвольного типового воздействия называют динамической ошибкой системы. В большинстве случаев при этом рассматривают моногармоническое воздействие

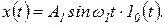
Как показано ранее, установившийся режим (вынужденные колебания) на выходе динамической линейной системы с по­стоянными параметрами может быть полностью охарактери­зован комплексной величиной

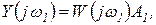
где 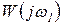— комплексный коэффициент усиления системы при частоте .

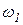Из (2.4.2) следует, что динамическая ошибка от управляю­щего воздействия

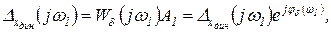(2.4.28)

где модуль

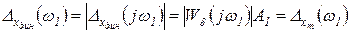(2.4.29)

равен амплитудному значению динамической ошибки системы или амплитудной погрешности, а аргумент

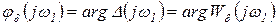(2.4.30)

— сдвигу фаз между динамической ошибкой и колебаниями на входе системы.

В функции времени

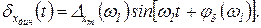(2.4.31)

Динамическая ошибка от возмущения f определяется аналогично, с заменой 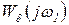на 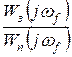, откуда

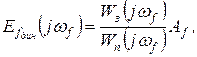(2.4.32)

где 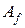— амплитуда синусоидального возмущения f;

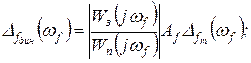(2.4.33)

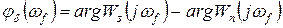(2.4.34)

и

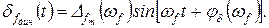(2.4.35)

Поскольку рассматриваются синусоидальные колебания, то среднеквадратичная ошибка или ее эффективное значение

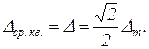(2.4.36)

Остановимся на оценке динамической точности системы автоматического регулирования, для которой 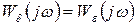. Структурная схема этой системы представлена на рисунке 2.4.4.

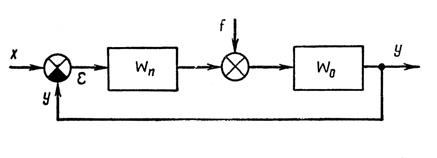
Рисунок 2.4.4 – Структурная схема системы автоматического управления

Аналитический расчёт модуля и фазы 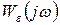для заданной частоты довольно трудоёмок и не всегда возможен, поскольку частотные характеристики объекта 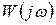часто даются в виде

В рабочем диапазоне ча­стот системы

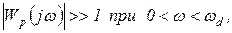(2.4.37)

где 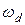— граничная частота равномерного пропускания замкнутой системы, опреде­ляемая из условия допустимых амплитудных искажений (рисунок 2.4.5) как меньший положительный корень уравнения

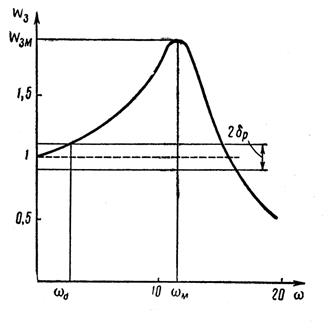
Рисунок 2.4.5 – Амплитудно-частотная характеристика замкнутой системы автоматического управления

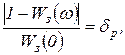(2.4.38)

в котором задается заранее. Обычно .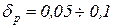

Неравенство (2.4.37) позволяет дать простую приближенную оценку динамической точности замкнутой системы по частотной характеристике разомкнутой системы. Действительно, в этом случае

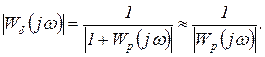(2.4.39)

Подставляя в (2.4.29), получаем

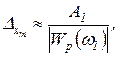(2.4.40)

где 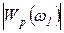— модуль комплексного коэффициента усиления разомкнутой системы при частоте управляющего воздействия .

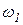Динамическая ошибка от возмущения (нагрузки) f определяется аналогично, при этом в рабочем диапазоне частот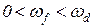

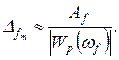(2.4.41)

Из (2.4.40) и (2.4.41) следует, что динамическая точность системы регулирования при отработке воздействий, частота кото­рых соответствует рабочему диапазону частот системы, тем выше, чем больше комплексный коэффициент усиления обрат­ной связи системы на частоте этого воздействия.