Интеграл Фурье. Преобразование Фурье
Определение:Функции, для которых существует  называют абсолютно интегрируемыми.
называют абсолютно интегрируемыми.
Пусть f(x) кусочно-непрерывная и абсолютно интегрируемая функция. На любом отрезке [-l;l]функция f(x) представима рядом Фурье.
Запишем ряд Фурье для f(x:
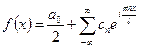 ,
, 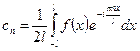 ,
,
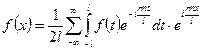 .
.
Введем обозначения 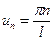 , получим
, получим
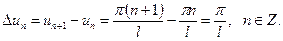
Тогда
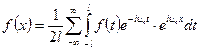 ,
,
учитывая, что 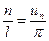 , получаем
, получаем
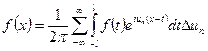
Последнее соотношение можно рассматривать как интегральную сумму для функции
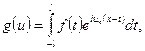
где 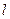 можно выбрать сколь угодно большим
можно выбрать сколь угодно большим 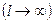 .
.
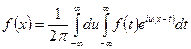 (1)
(1)
это интеграл Фурье в комплексной форме. Преобразуем его к следующему виду:
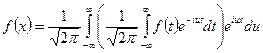
Получим соотношения:
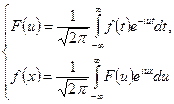 (2)
(2)
Это – преобразования Фурье F(u) прямое преобразование Фурье f(x) обратное преобразование Фурье.
Но, согласно формуле Эйлера, 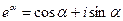 , то есть
, то есть
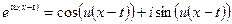 .
.
Подставим в интеграл Фурье:
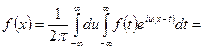
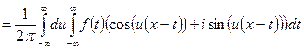 . (3)
. (3)
Соотношение (3) - это интеграл Фурье в вещественной форме. С учётом того, что
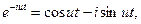
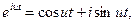
Преобразования Фурье принимают вид:
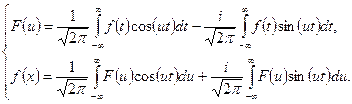 (4)
(4)
Если f(x) нечётная, то
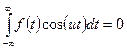
следовательно,
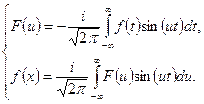
Или, введя обозначения
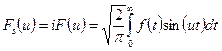 , (5)
, (5)
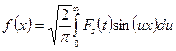 . (6)
. (6)
Формулы (5), (6) называют синус-преобразованием Фурье.
Если f(x) - чётная, то
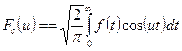 , (7)
, (7)
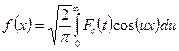 . (8)
. (8)
Формулы (7), (8) называют косинус-преобразованием Фурье.
Пример:
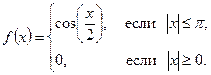
Функция f(x) - чётная. Следовательно,
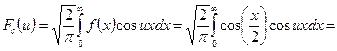
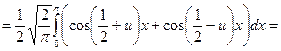
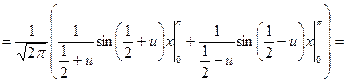
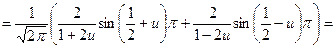
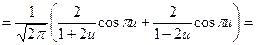
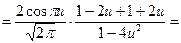
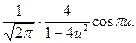
Дата добавления: 2015-08-11; просмотров: 846;
