Z-преобразование и его свойства
Z-преобразование в ЦСАУ имеет такое же важное значение, как преобразование Лапласа в теории непрерывных систем.
Пусть 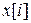 , i =0, 1, 2,...- полубесконечная числовая последовательность.
, i =0, 1, 2,...- полубесконечная числовая последовательность.
Z-преобразование этой последовательности определяется как
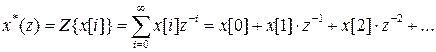 ,
,
где Z-символ (оператор) Z-преобразования,
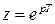 - комплексная переменная Z-преобразования, причем
- комплексная переменная Z-преобразования, причем 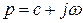 , Т – период дискретизации.
, Т – период дискретизации.
Z-преобразование существует для 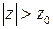 ,
, 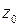 — радиус абсолютной сходимости ряда в правой части выражения для
— радиус абсолютной сходимости ряда в правой части выражения для 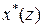 .
.
Найдем Z- преобразование единичной последовательности 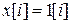 :
:
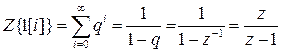 ,
, 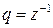 ,
,
где 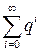 - сумма убывающей геометрической прогрессии.
- сумма убывающей геометрической прогрессии.
Это преобразование существует для 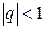 .
.
Краткая таблица Z- преобразований
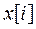
| 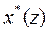
|
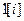
| 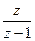
|
| i | 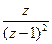
|
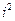
| 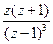
|
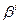
| 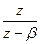
|
Дата добавления: 2015-08-14; просмотров: 1791;
