Уравнения объекта, управляемого от ЦВМ, в переменных состояния

Рассмотрим последовательное соединение ЦАП, объекта управления и АЦП (рис. 6), входящих в функциональную схему цифровой системы управления. При этом будем считать, что u[i] является r-векторной управляющей последовательностью, a y[i] - l-векторной управляемой последовательностью, другими словами, будем считать объект управления многомерным, имеющим r входных и l выходных сигналов. Кроме того,

предположим, что известны уравнения объекта в переменных состояния

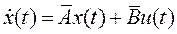, (2)

,

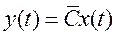связывающие управляемый y(t) и управляющий u(t) сигналы. Здесь 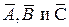- матрицы соответственно размерностью 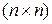, 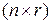и 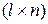, n - размерность вектора состояния объекта х(t), иначе - порядок объекта управления.

Для получения математической модели такого соединения надо, прежде всего, найти описание преобразователей АЦП и ЦАП.

Описание ЦАП. С ЦВМ на вход ЦАП поступает векторный цифровой сигнал с периодом дискретизации Т, моделью которого является управляющая

последовательность u[i].

ЦАП преобразует такой цифровой сигнал в непрерывный управляющий сигнал u(t), используя выражение

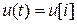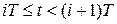, . (3)

Отсюда процесс цифроаналогового преобразования можно интерпретировать как сохранение постоянного уровня управляющего сигнала между моментами дискретизации (рис.7). В результате преобразования образуется сигнал u(t) "ящичного" типа.

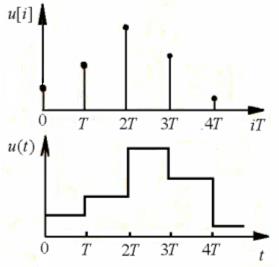
Рис. 7

Таким образом, математической моделью ЦАП можно считать устройство, "растягивающее" каждое значение управляющей последовательности u[i] на период дискретизации, т.е. до прихода следующего значения, и описываемое (3). Подобное устройство принято называть фиксатором или экстраполятором нулевого порядка и схематически обозначать в виде, изображенном на рис. 8. Фактически на выходе фиксатора получаем не сам непрерывный сигнал u(t), который поступает на АЦП, а его аппроксимацию 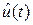(рис. 7,а).

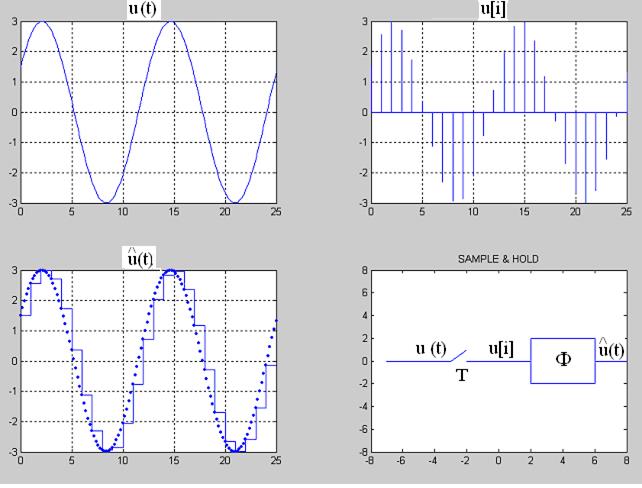
Рис. 7,а

Описание АЦП. АЦП оперирует непрерывным сигналом - управляемой величиной y(t), получаемой с выхода объекта управления, и преобразует этот сигнал в цифровой сигнал - последовательность кодовых групп импульсов, появляющихся в моменты .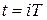

Абстрагируясь от физического носителя информации об управляемой величине, можно принять в качестве математической модели АЦП устройство, преобразующее управляемую величину y(t) в числовую управляемую последовательность .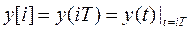

Такое устройство называется ключом или дискретизатором и обозначается на схемах в виде, представленном на рис. 9.

Следовательно, математическую модель последовательного соединения ЦАП - объект управления - АЦП можно представить, как показано на рис. 10 .

Нетрудно видеть, что такое соединение эквивалентно дискретному фильтру, входом и выходом которого являются соответственно управляющая u[i] и управляемая y[i] последовательности.

Поставим задачу: найти разностные уравнения в переменных состояния, связывающие управляемую y[i] и управляющую u[i] последовательности. Как известно, решение уравнения состояния 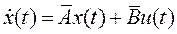(2) имеет вид

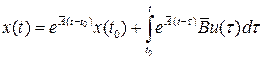, (4)

где 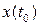- начальное состояние, т.е. значение вектора состояния в момент 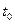. Положим 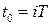, 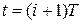. Учитывая также, что в промежутки между моментами дискретизации управляющий сигнал, снимаемый с выхода фиксатора, постоянен, т.е.

, ,

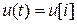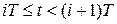из (4) получаем

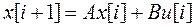, (5)

где

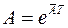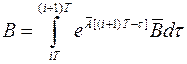, . (6)

Введя другую переменную интегрирования 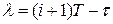, так что 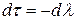, приводим выражение для матрицы В к более простому виду

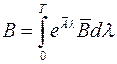. (7)

Полагая в уравнении выхода 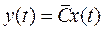(2) 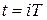, , 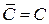получаем

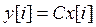. (8)

Система уравнений (5) и (8) образует уравнения в переменных состояния объекта, управляемого ЦВМ.

Таким образом, поведение объекта, управляемого ЦВМ, описывается уравнениями, не отличающимися от уравнений (1) в параграфе 3.8, что позволяет рассматривать этот объект как эквивалентный дискретный фильтр. Матрицы А и В разностного уравнения состояния находят по известным матрицам 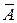и 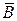аналитическим путем, используя теорему Кэли-Гамильтона, согласно которой

,

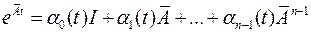где коэффициенты 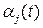определяются соответствующими приемами, или используя разложение экспоненциальной функции в ряд

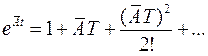
При этом вычисление последующих членов разложения прекращают, когда добавки мало влияют на значение правой части матрицы 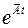. Еще один метод основан на формуле

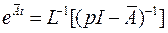, (9)

где 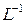- оператор обратного преобразования Лапласа.

Лекция 14

Пример. Пусть объект управления представляет собой двойной интегратор с одним входом u(t) и одним выходом y(t), описываемый уравнениями в переменных состояния

, .

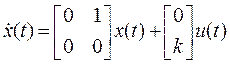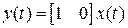В данном случае

, .

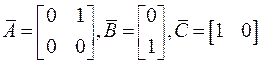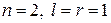Найдем векторные разностные уравнения этого объекта при управлении от ЦВМ.

Учитывая, что

и используя 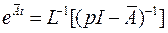(9), получаем

.

Следовательно,

.

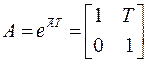Так как

,

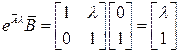то в соответствии с 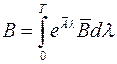(7)

.

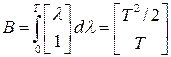Согласно 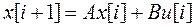(5) и 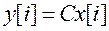(8) искомые разностные уравнения в переменных состояния имеют вид

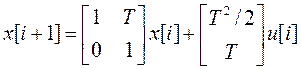(10)

.

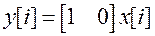Заметим, что элементы матриц А и В, входящих в уравнение (10), не только в этом примере, но и в общем случае зависят от периода дискретизации Т. Поэтому для их обозначения иногда используют выражения А(Т), В(Т).

Если объект управления имеет один вход и один выход, то его разностные уравнения в переменных состояния можно найти другим способом, а именно, в начале определить дискретную передаточную функцию объекта (см. ниже), затем найти разностное уравнение n порядка, связывающее у[i] и u[i], и, наконец, преобразовать последнее в векторные разностные уравнения.

В дальнейшем последовательное соединение фиксатора, объекта и ключа (рис. 4) будем называть управляемой цифровой системой или просто цифровой системой.