Передаточная функция цифровой системы.

Передаточную функцию цифровой системы можно определить двояко, или по разностным уравнениям или по передаточной функции ОУ.

Первый способ. Найдем Z-преобразование разностного уравнения состояния 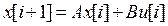(11):

,

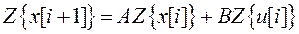Следует отметить, что все теоремы и свойства Z-преобразования для скалярных последовательностей справедливы по отношению к векторным последовательностям.

Используя теорему смещения

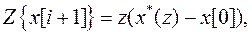
где 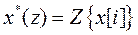есть Z-преобразование вектора состояния, после простых преобразований получаем

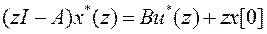. (18)

Здесь 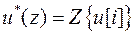- Z-преобразование управляющей (входной) последовательности, а I - единичная матрица ( 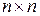), x[0] - начальное состояние, представляющее начальные условия для разностного уравнения состояния. Введя в рассмотрение дискретную резольвенту

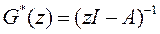, (19)

после умножения ее слева на 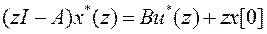(18) находим

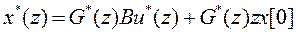. (20)

Z-преобразование выходной последовательности с учетом уравнения 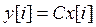(12)

.

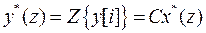Подставляя 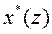из (20), получаем

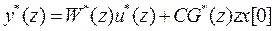, (21)

где матрица

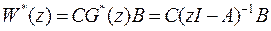(22)

размерностью ( 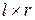) называется матричной передаточной функцией цифровой системы. Она связывает Z-преобразования выхода и входа предварительно невозбужденной цифровой системы, т.е. при x[0]=0,

.

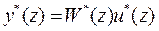Если 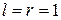(Д-фильтр с одним входом и одним выходом), то матрица 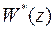вырождается в скалярную передаточную функцию, которая является отношением многочленов от z:

.

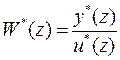В соответствии с 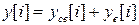(14), 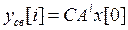(15) и (16) управляемая, другими словами, выходная последовательность (реакция) цифровой системы имеет вид

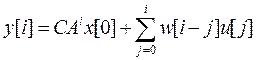. (23)

Находя Z-преобразование этого уравнения, с учетом теоремы об изображения суммы свертки получаем

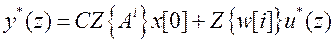. (24)

Сравнивая выражения 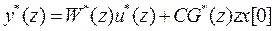(21) и (24), определяем, что

,

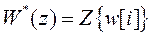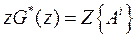. (25)

Отсюда

,

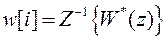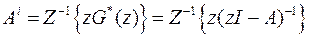. (26)

Таким образом, матричные передаточная функция и весовая последовательность, связаны между собой как Z-изображение и оригинал, а матрицу 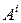можно найти с помощью обратного Z-преобразования 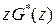, минуя возведение матрицы А в степень i.

В разделе Пространство состояний в теории управления мы доказали, что резольвенту непрерывной системы 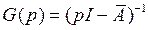можно представить в виде отношения матричного полинома и характеристического (скалярного) полинома :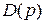

,

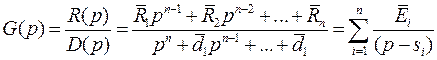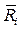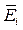где и - матричные коэффициенты, 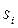- корни характеристического уравнения матрицы :

.

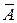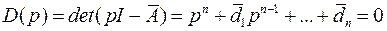Аналогичным путем нетрудно показать, что дискретную резольвенту 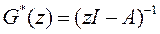можно представить в виде отношения матричного полинома 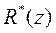и характеристического полинома (скалярного) :

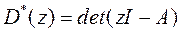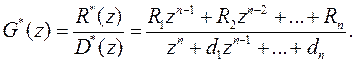(27)

Полагая известными собственные значения 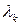матрицы А, другими словами, корни характеристического уравнения системы 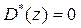, и считая, что все корни простые, получаем

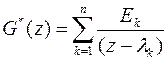, (27a)

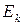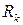где и – матричные коэффициенты.

Если подставить в выражение (22) 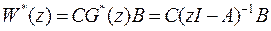для матричной ПФ выражение (27) для дискретной резольвенты, то нетрудно найти, что

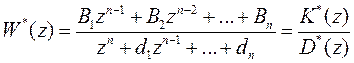. (28)

Здесь 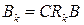, 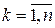- постоянные матрицы. Если r=l=1, то матричный полином вырождается в скалярный полином

,

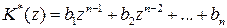где 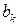, 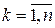- постоянные коэффициенты.

Пример. Найдем передаточную функцию двойного интегратора, управляемого от ЦВМ и описываемого векторными разностными уравнениями (10) 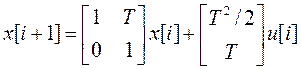, , 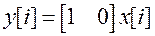из которых следует, что

, .

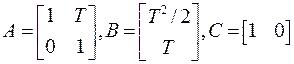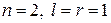Учитывая, что

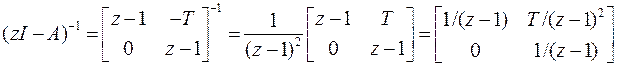
и используя (22) 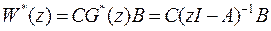, получаем