Реализация передаточной функции в пространстве состояний.

Разумеется, описание

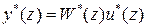(32)

системы с помощью передаточных функций может быть и исходным; иногда оно возникает более естественно, чем описание в пространстве состояний.

В этой записи под передаточной функцией 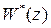будем понимать матрицу 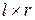, элементы которой есть дробно-рациональные функции от z, т.е. передаточная функция представима в виде

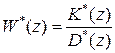, (33)

где элементы 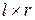матрицы являются полиномами от z. Полином 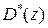- общий знаменатель элементов матрицы 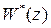- будем называть характеристическим полиномом системы, a его корни — полюсами передаточной функции (системы). Такое определение характеристического полинома и полюсов системы не вполне точно, поскольку могут возникнуть неприятности, связанные, например, с возможным сокращением неустойчивых полюсов (см. обсуждение ниже). Более строгое определение дается следующим образом.

Формально умножив обе части (32) на 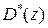, с учетом (33) получаем

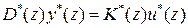(34)

и, рассматривая теперь z как оператор прямого сдвига Е, приходим к системе разностных уравнений высокого порядка относительно y[i], u[i]. На элементы матрицы естественно накладывается дополнительное условие физической осуществимости (реализуемости): степень полинома в числителе не превосходит степени полинома в знаменателе; такие передаточные функции будем называть правильными или физически осуществимыми (реализуемыми). Тогда, вводя «искусственные» переменные состояния, можно привести уравнение (34) к виду, аналогичному (11 - 12). Иными словами, от записи системы с помощью реализуемой передаточной функции можно перейти к эквивалентному описанию в пространстве состояний, которое принято называть реализацией передаточной функции в пространстве состояний или ( А, В, С)–реализацией.

При этом система, описываемая уравнением (32), эквивалентна системе:

, ,

,

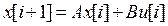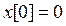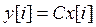и

.

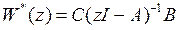Переход от 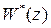к (А, В, С) - реализации может быть осуществлен различными способами, и таких реализаций много. Среди них существуют такие, в которых размерность А (т. е. размерность вектора состояний х) минимальна; они называются минимальными реализациями. Соответствующая размерность А называется степенью Мак-Миллана для передаточной функции. Эта степень может быть найдена с помощью специального алгоритма – приведения 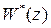к так называемой форме Мак-Миллана. Если (А,В,С) - минимальная реализация 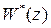, то

представляет собой характеристический полином системы, а его корни - собственные значения матрицы А — называются полюсами матричной передаточной функции (полюсами системы).

Команда MATLAB: minreal(sys) - построение минимальной реализации для передаточной функции.

Читать